| << Chapter < Page | Chapter >> Page > |
where and
Determine whether and are equivalent vectors, where and
Equivalent vectors
Determine whether the vectors and are equivalent, where and
For the following exercises, find vector with a magnitude that is given and satisfies the given conditions.
and have the same direction
and have opposite directions for any where is a real number
Determine a vector of magnitude in the direction of vector where and
Find a vector of magnitude that points in the opposite direction than vector where and Express the answer in component form.
Consider the points and where and are negative real numbers. Find and such that
Consider points and where and are positive real numbers. Find and such that
Let be a point situated at an equal distance from points and Show that point lies on the plane of equation
Let be a point situated at an equal distance from the origin and point Show that the coordinates of point satisfy the equation
The points and are collinear (in this order) if the relation is satisfied. Show that and are collinear points.
Show that points and are not collinear.
[T] A force of acts on a particle in the direction of the vector where
a. b.
[T] A force of acts on a box in the direction of the vector where
If is a force that moves an object from point to another point then the displacement vector is defined as A metal container is lifted m vertically by a constant force Express the displacement vector by using standard unit vectors.
A box is pulled yd horizontally in the x -direction by a constant force Find the displacement vector in component form.
The sum of the forces acting on an object is called the resultant or net force . An object is said to be in static equilibrium if the resultant force of the forces that act on it is zero. Let and be three forces acting on a box. Find the force acting on the box such that the box is in static equilibrium. Express the answer in component form.
[T] Let be forces acting on a particle, with
The force of gravity acting on an object is given by where m is the mass of the object (expressed in kilograms) and is acceleration resulting from gravity, with A 2-kg disco ball hangs by a chain from the ceiling of a room.

a. N; b. N
A 5-kg pendant chandelier is designed such that the alabaster bowl is held by four chains of equal length, as shown in the following figure.

[T] A 30-kg block of cement is suspended by three cables of equal length that are anchored at points and The load is located at as shown in the following figure. Let and be the forces of tension resulting from the load in cables and respectively.
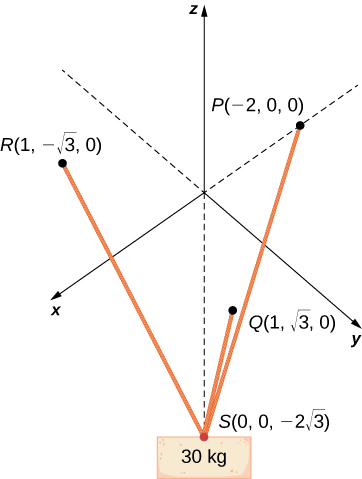
a. N; b. and (each component is expressed in newtons)
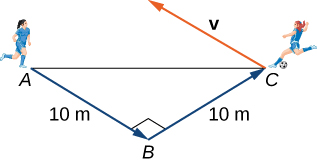
Two soccer players are practicing for an upcoming game. One of them runs 10 m from point A to point B . She then turns left at and runs 10 m until she reaches point C . Then she kicks the ball with a speed of 10 m/sec at an upward angle of to her teammate, who is located at point A . Write the velocity of the ball in component form.
Let be the position vector of a particle at the time where and are smooth functions on The instantaneous velocity of the particle at time is defined by vector with components that are the derivatives with respect to of the functions x , y , and z , respectively. The magnitude of the instantaneous velocity vector is called the speed of the particle at time t. Vector with components that are the second derivatives with respect to of the functions and respectively, gives the acceleration of the particle at time Consider the position vector of a particle at time where the components of are expressed in centimeters and time is expressed in seconds.
a. (each component is expressed in centimeters per second); (expressed in centimeters per second); (each component expressed in centimeters per second squared);
b.
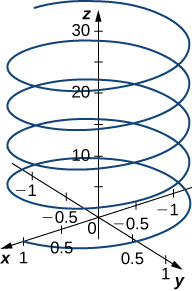
[T] Let be the position vector of a particle at time (in seconds), where (here the components of are expressed in centimeters).

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?