| << Chapter < Page | Chapter >> Page > |
Anna and Emanuel start at the same intersection. Anna walks east at 4 miles per hour while Emanuel walks south at 3 miles per hour. They are communicating with a two-way radio that has a range of 2 miles. How long after they start walking will they fall out of radio contact?
In essence, we can partially answer this question by saying they will fall out of radio contact when they are 2 miles apart, which leads us to ask a new question:
In this problem, our changing quantities are time and position, but ultimately we need to know how long will it take for them to be 2 miles apart. We can see that time will be our input variable, so we’ll define our input and output variables.
Because it is not obvious how to define our output variable, we’ll start by drawing a picture such as [link] .
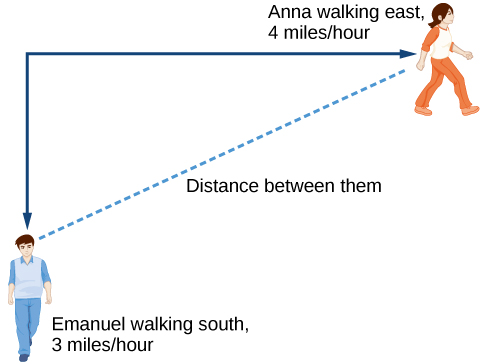
Initial Value: They both start at the same intersection so when the distance traveled by each person should also be 0. Thus the initial value for each is 0.
Rate of Change: Anna is walking 4 miles per hour and Emanuel is walking 3 miles per hour, which are both rates of change. The slope for is 4 and the slope for is 3.
Using those values, we can write formulas for the distance each person has walked.
For this problem, the distances from the starting point are important. To notate these, we can define a coordinate system, identifying the “starting point” at the intersection where they both started. Then we can use the variable, which we introduced above, to represent Anna’s position, and define it to be a measurement from the starting point in the eastward direction. Likewise, can use the variable, to represent Emanuel’s position, measured from the starting point in the southward direction. Note that in defining the coordinate system, we specified both the starting point of the measurement and the direction of measure.
We can then define a third variable, to be the measurement of the distance between Anna and Emanuel. Showing the variables on the diagram is often helpful, as we can see from [link] .
Recall that we need to know how long it takes for the distance between them, to equal 2 miles. Notice that for any given input the outputs and represent distances.
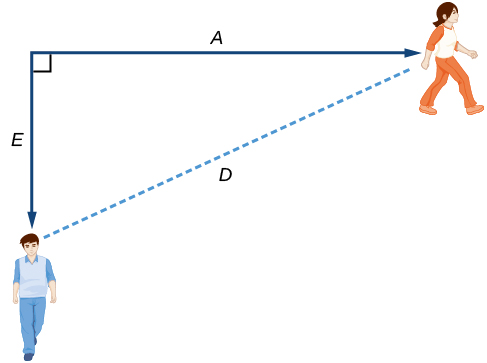
[link] shows us that we can use the Pythagorean Theorem because we have drawn a right angle.
Using the Pythagorean Theorem, we get:
In this scenario we are considering only positive values of so our distance will always be positive. We can simplify this answer to This means that the distance between Anna and Emanuel is also a linear function. Because is a linear function, we can now answer the question of when the distance between them will reach 2 miles. We will set the output and solve for
They will fall out of radio contact in 0.4 hours, or 24 minutes.

Notification Switch
Would you like to follow the 'Essential precalculus, part 1' conversation and receive update notifications?