2.2 Introduction to the mos transistor and mosfets  (Page 2/2)

Now we can go back now to our initial structure, shown in [link] , only this time we will add an oxide layer, a gate structure, and another battery so that we can invert theregion under the gate and connect the two n-regions together. Well also identify some names for parts of thestructure, so we will know what we are talking about. For reasons which will be clear later, we call the n-regionconnected to the negative side of the battery the source, and the other one thedrain. We will ground the source, and also the p-type substrate. We add two batteries, $V_{\mathrm{gs}}$ between the gate and the source, and $V_{\mathrm{ds}}$ between the drain and the source.

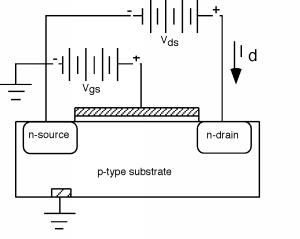
It will be helpful if we also make another sketch, which givesus a perspective view of the device. For this we strip off the gate and oxide, but we will imagine that we have applied avoltage greater than $V_T$ to the gate, so there is a n-type region, called the channel which connects thetwo. We will assume that the channel region is $L$ long and $W$ wide, as shown in [link] .

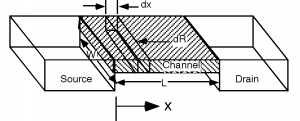
Next we want to take a look at a little section of channel, and find its resistance $d(R)$ , when the little section is $d(x)$ long, [link] .

We have introduced a slightly different form for our resistance formula here. Normally, we would have asimple $\sigma$ in the denominator, and an area $A$ , for the cross-sectional area of the channel. It turns out to be veryhard to figure out what that cross sectional area of the channel is however. The electrons which form the inversion layer crowdinto a very thin sheet of surface charge which really has little or no thickness, or penetration into thesubstrate.

If, on the other hand we consider a surface conductivity (units: simply mhos), ${\sigma }_s$ , [link] , then we will have an expression which we can evaluate. Here, ${\mu }_s$ is a surface mobility, with units of cm ² /V.sec, that is the quantity which represented the proportionality between the average carriervelocity and the electric field, [link] and [link] .

The surface mobility is a quantity which has to be measured for a given system, and is usually just a number which is given toyou. Something around 300 cm ² /V.sec is about right for silicon. $Q_{\mathrm{chan}}$ is called the surface charge density or channel charge density and it has units of Coulombs/cm ² . This is like a sheet of charge, which is different from the bulkcharge density, which has units of Coulombs/cm ² . Note that:

It turns out that it is pretty simple to get an expression for $Q_{\mathrm{chan}}$ , the surface charge density in the channel. For any given gate voltage $V_{\mathrm{gs}}$ , we know that the charge density on the gate is given simply as:

However, until the gate voltage $V_{\mathrm{gs}}$ gets larger than $V_T$ we are not creating any mobile electrons under the gate, we are just building up a depletionregion. We'll define $Q_T$ as the charge on the gate necessary to get to threshold. $Q_T=c_{\mathrm{ox}}{V}_T$ . Any charge added to the gate above $Q_T$ is matched by charge $Q_{\mathrm{chan}}$ in the channel. Thus, it is easy to say: [link] or [link] .

Thus, putting [link] and [link] into [link] , we get:

If you look back at [link] , you will see that we have defined a current $I_d$ flowing into the drain. That current flows through the channel, and hence through our littleincremental resistance $d(R)$ , creating a voltage drop $d(V_c)$ across it, where $V_c$ is the channel voltage, [link] .

Let's move the denominator to the left, and integrate. We want to do our integral completely along the channel. The voltage onthe channel $V_c(x)$ goes from 0 on the left to $V_{\mathrm{ds}}$ on the right. At the same time, $x$ is going from 0 to $L$ . Thus our limits of integration will be 0 and $V_{\mathrm{ds}}$ for the voltage integral $d(V_c(x))$ and from 0 to $L$ for the $x$ integral $d(x)$ .

Both integrals are pretty trivial. Let's swap the equation order, since we usually want $I_d$ as a function of applied voltages.

We now simply divide both sides by $L$ , and we end up with an expression for the drain current $I_d$ , in terms of the drain-source voltage, $V_{\mathrm{ds}}$ , the gate voltage $V_{\mathrm{gs}}$ and some physical attributes of the MOS transistor.