| << Chapter < Page | Chapter >> Page > |
Rather than looking at an example of the washer method with the as the axis of revolution, we now consider an example in which the axis of revolution is a line other than one of the two coordinate axes. The same general method applies, but you may have to visualize just how to describe the cross-sectional area of the volume.
Find the volume of a solid of revolution formed by revolving the region bounded above by and below by the over the interval around the line
The graph of the region and the solid of revolution are shown in the following figure.
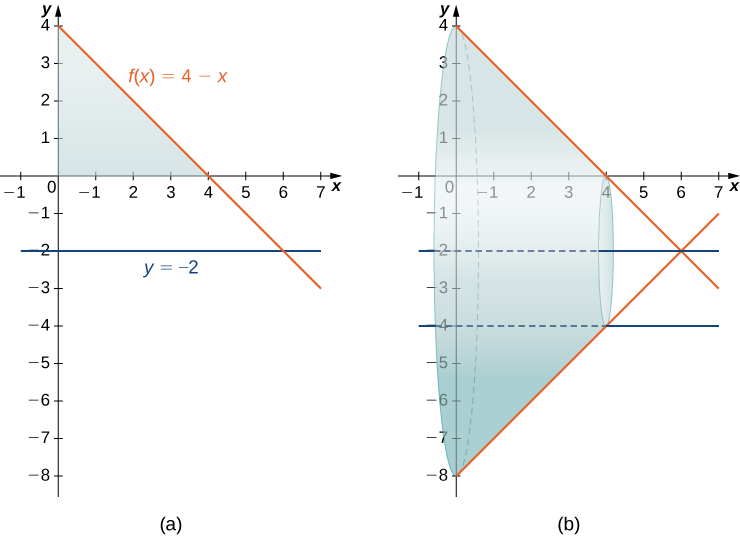
We can’t apply the volume formula to this problem directly because the axis of revolution is not one of the coordinate axes. However, we still know that the area of the cross-section is the area of the outer circle less the area of the inner circle. Looking at the graph of the function, we see the radius of the outer circle is given by which simplifies to
The radius of the inner circle is Therefore, we have
Find the volume of a solid of revolution formed by revolving the region bounded above by the graph of and below by the over the interval around the line
units 3
Derive the formula for the volume of a sphere using the slicing method.
Use the slicing method to derive the formula for the volume of a cone.
Use the slicing method to derive the formula for the volume of a tetrahedron with side length
Use the disk method to derive the formula for the volume of a trapezoidal cylinder.
Explain when you would use the disk method versus the washer method. When are they interchangeable?
For the following exercises, draw a typical slice and find the volume using the slicing method for the given volume.
A pyramid with height 6 units and square base of side 2 units, as pictured here.
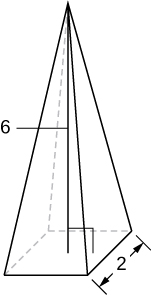
8 units 3
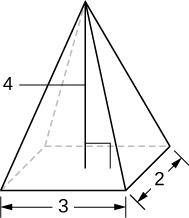
A pyramid with height 4 units and a rectangular base with length 2 units and width 3 units, as pictured here.

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?