| << Chapter < Page | Chapter >> Page > |
Activity 1:
To compare fractions [LO 1.3]
1. Each of the following three bars represents one whole.
The top bar shows thirds. The middle bar shows twelfths. The last bar shows sixths. You may use them to replace with the correct sign from:<and to make the statements true:
1.1
1.2
1.3
1.4
2. Here again, each of the bars represents one whole.
The top bar shows . The lower bar shows .
You may use these bars to complete the following:
3. Here again, each of the bars represents one whole.
Look carefully at the bars above and then complete the following:
Activity 2:
To count forwards and backwards in fractions [LO 1.3]
1. Group Discussion
Read the following and discuss who was correct:
The educator said, “Count in halves from 0 to 10.”
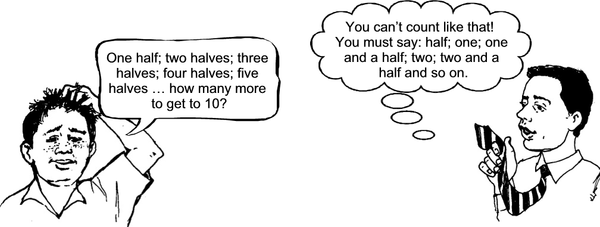
Who was correct?
Actually both ways of counting were correct. Let’s look at the way Peter did it.
; ; ; ; What do you notice?
Yes, after the first two, the top part of the fraction is bigger than the bottom part.
What does this mean? Discuss.
Yes, it means that there is at least one whole hidden in there.
= one whole; = What do four halves mean? What do five halves mean?
When the top part of the fraction is larger than the bottom part, we call it an IMPROPER FRACTION.
is an IMPROPER FRACTION; the top bit is larger than the bottom bit.
Sometimes it is necessary to make improper fractions in calculations. However, most educators like the final answer to a calculation to be a mixed number.
2. ORAL WORK: Now do these counting exercises. You may use either improper fractions or mixed numbers. Ask a friend to check your answers.
2.1 (a) Count in halves from 0 to 10.
(b) Count backwards in halves from 100 to 90
2.2 (a) Count in thirds from 6 to 10.
(b) Count backwards in thirds from 30 to 25.
2.3 (a) Count in quarters from 12 to 16.
(b) Count backwards in quarters from 100 to 96.
2.4 (a) Count in fifths from 50 to 55.
(b) Count backwards in fifths from 10 to 6.
2.5 (a) Count in sixths from 24 to 26.
(b) Count backwards in sixths from 36 to 30.
2.6 (a) Count in sevenths from 0 to 4.
(b) Count backwards in sevenths from 21 to 17.
2.7 (a) Count in eighths from 0 to 3.
(b) Count backwards in eighths from 10 to 8.
2.8 (a) Count in tenths from 3 to 8.
(b) Count backwards in tenths from 100 to 97.
Activity 3:
To recognise equivalent fractions [LO 1.5, 2.1]
Two boys study a measuring beaker half full:

Who is correct? Yes, they both are. There is only one beaker and one quantity of Coke, but it can be called and ; thus, different names for the same quantity.
We say and are EQUIVALENT FRACTIONS.
The thousandths are smaller pieces, but there are 500 of them; enough to make a half.

Notification Switch
Would you like to follow the 'Mathematics grade 4' conversation and receive update notifications?