| << Chapter < Page | Chapter >> Page > |
In this module some of the basic classifications of systems will be briefly introduced and the most important propertiesof these systems are explained. As can be seen, the properties of a system provide an easy way to separate onesystem from another. Understanding these basic difference's between systems, and their properties, will be a fundamentalconcept used in all signal and system courses, such as digital signal processing (DSP). Once a set of systems can beidentified as sharing particular properties, one no longer has to deal with proving a certain characteristic of a system eachtime, but it can simply be accepted do the systems classification. Also remember that this classificationpresented here is neither exclusive (systems can belong to several different classifications) nor is it unique.
Along with the classification of systems below, it is also important to understand other Classification of Signals .
This may be the simplest classification to understand as the idea of discrete-time and continuous-time is one of the mostfundamental properties to all of signals and system. A system where the input and output signals are continuous is a continuous system , and one where the input and output signals are discrete is a discrete system .
A linear system is any system that obeys the properties of scaling (homogeneity) and superposition(additivity), while a nonlinear system is any system that does not obey at least one of these.
To show that a system obeys the scaling property is to show that

To demonstrate that a system obeys the superposition property of linearity is to show that

It is possible to check a system for linearity in a single (though larger) step. To do this, simply combine the firsttwo steps to get
A time invariant system is one that does not depend on when it occurs: the shape of the output does notchange with a delay of the input. That is to say that for a system where , is time invariant if for all

When this property does not hold for a system, then it is said to be time variant , or time-varying.
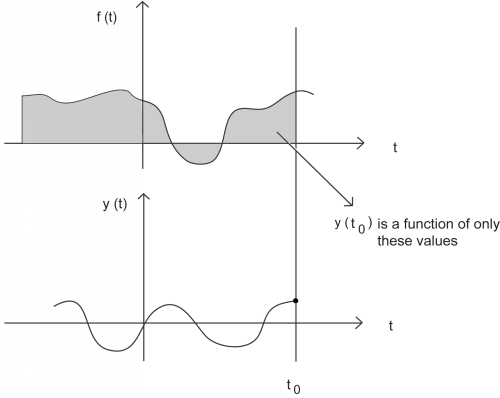
A causal system is one that is nonanticipative ; that is, the output may depend on current and past inputs, but not future inputs. All"realtime" systems must be causal, since they can not have future inputs available to them.
One may think the idea of future inputs does not seem to make much physical sense; however, we have only beendealing with time as our dependent variable so far, which is not always the case. Imagine rather that we wanted to doimage processing. Then the dependent variable might represent pixels to the left and right (the "future") of the currentposition on the image, and we would have a noncausal system.

A stable system is one where the output does not diverge as long as the input does not diverge. Thereare many ways to say that a signal "diverges"; for example it could have infinite energy. One particularly usefuldefinition of divergence relates to whether the signal is bounded or not. Then a system is referred to as bounded input-bounded output (BIBO) stable if every possible bounded input produces a bounded output.
Representing this in a mathematical way, a stable system must have the following property, where is the input and is the output. The output must satisfy the condition
If these conditions are not met,

Notification Switch
Would you like to follow the 'Principles of digital communications' conversation and receive update notifications?