| << Chapter < Page | Chapter >> Page > |
| Material | Index of Refraction |
|---|---|
| Water | 1.33 |
| Air | 1.0 |
| Cornea | 1.38 |
| Aqueous humor | 1.34 |
| Lens | 1.41 average (varies throughout the lens, greatest in center) |
| Vitreous humor | 1.34 |
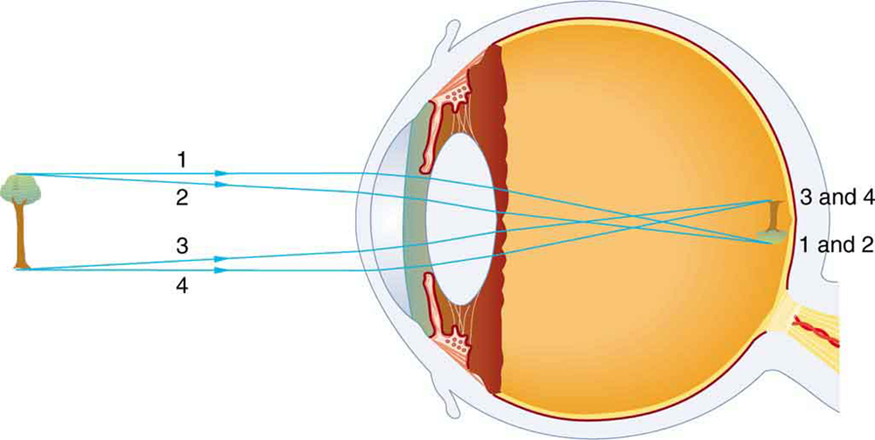
As noted, the image must fall precisely on the retina to produce clear vision — that is, the image distance must equal the lens-to-retina distance. Because the lens-to-retina distance does not change, the image distance must be the same for objects at all distances. The eye manages this by varying the power (and focal length) of the lens to accommodate for objects at various distances. The process of adjusting the eye’s focal length is called accommodation . A person with normal (ideal) vision can see objects clearly at distances ranging from 25 cm to essentially infinity. However, although the near point (the shortest distance at which a sharp focus can be obtained) increases with age (becoming meters for some older people), we will consider it to be 25 cm in our treatment here.
[link] shows the accommodation of the eye for distant and near vision. Since light rays from a nearby object can diverge and still enter the eye, the lens must be more converging (more powerful) for close vision than for distant vision. To be more converging, the lens is made thicker by the action of the ciliary muscle surrounding it. The eye is most relaxed when viewing distant objects, one reason that microscopes and telescopes are designed to produce distant images. Vision of very distant objects is called totally relaxed , while close vision is termed accommodated , with the closest vision being fully accommodated .
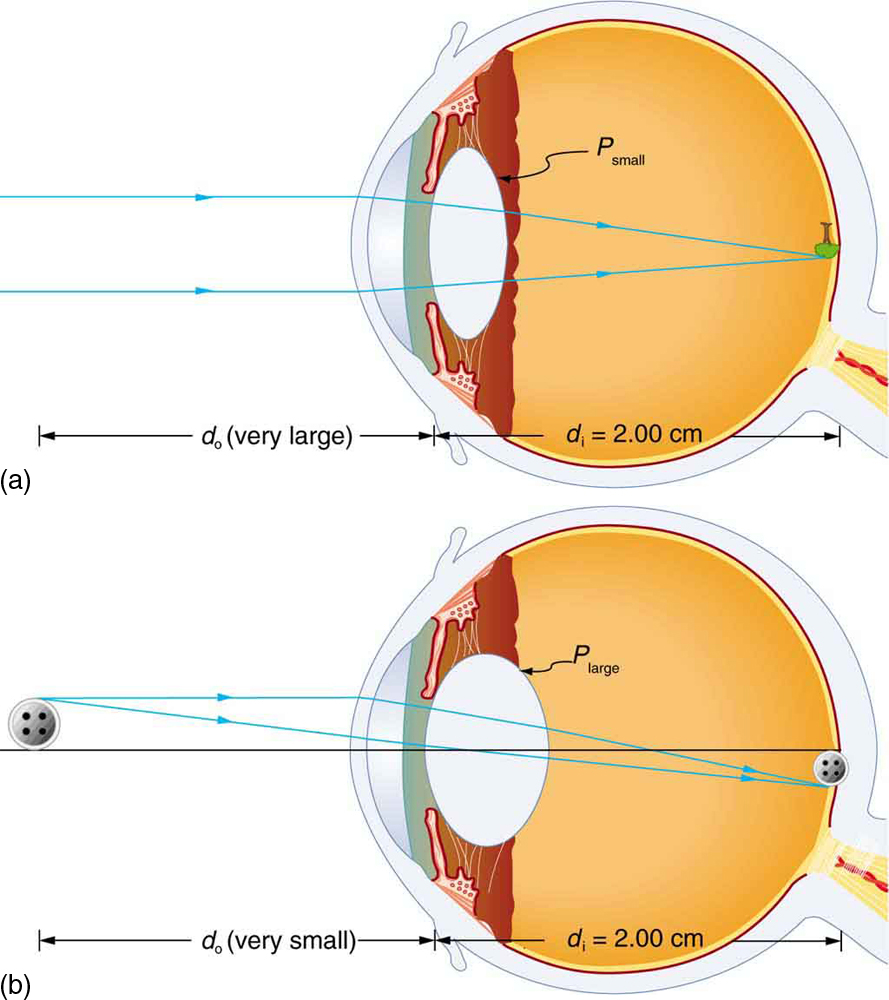
We will use the thin lens equations to examine image formation by the eye quantitatively. First, note the power of a lens is given as , so we rewrite the thin lens equations as
and
We understand that must equal the lens-to-retina distance to obtain clear vision, and that normal vision is possible for objects at distances to infinity.
Look at the central transparent area of someone’s eye, the pupil, in normal room light. Estimate the diameter of the pupil. Now turn off the lights and darken the room. After a few minutes turn on the lights and promptly estimate the diameter of the pupil. What happens to the pupil as the eye adjusts to the room light? Explain your observations.

Notification Switch
Would you like to follow the 'Physics for the modern world' conversation and receive update notifications?