| << Chapter < Page | Chapter >> Page > |
For the next three exercises, use the data to construct a line graph.
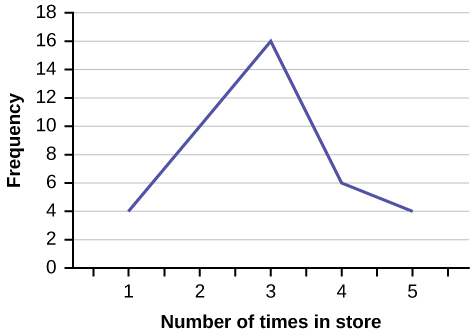
In a survey, 40 people were asked how many times they visited a store before making a major purchase. The results are shown in [link] .
| Number of times in store | Frequency |
|---|---|
| 1 | 4 |
| 2 | 10 |
| 3 | 16 |
| 4 | 6 |
| 5 | 4 |
In a survey, several people were asked how many years it has been since they purchased a mattress. The results are shown in [link] .
| Years since last purchase | Frequency |
|---|---|
| 0 | 2 |
| 1 | 8 |
| 2 | 13 |
| 3 | 22 |
| 4 | 16 |
| 5 | 9 |
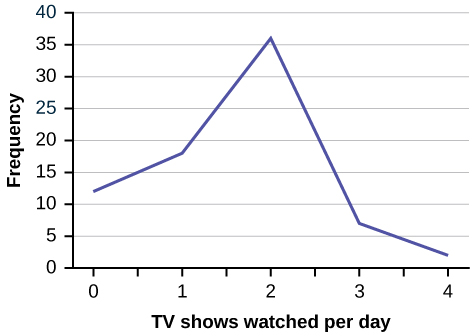
Several children were asked how many TV shows they watch each day. The results of the survey are shown in [link] .
| Number of TV Shows | Frequency |
|---|---|
| 0 | 12 |
| 1 | 18 |
| 2 | 36 |
| 3 | 7 |
| 4 | 2 |
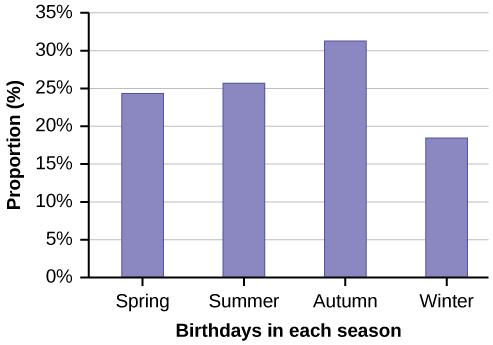
The students in Ms. Ramirez’s math class have birthdays in each of the four seasons. [link] shows the four seasons, the number of students who have birthdays in each season, and the percentage (%) of students in each group. Construct a bar graph showing the number of students.
| Seasons | Number of students | Proportion of population |
|---|---|---|
| Spring | 8 | 24% |
| Summer | 9 | 26% |
| Autumn | 11 | 32% |
| Winter | 6 | 18% |
Using the data from Mrs. Ramirez’s math class supplied in [link] , construct a bar graph showing the percentages.
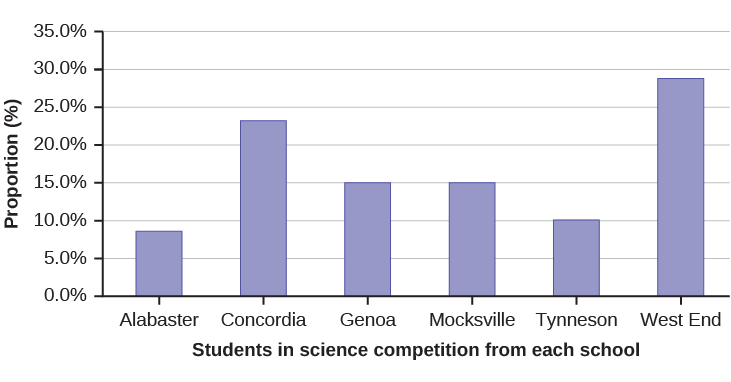
David County has six high schools. Each school sent students to participate in a county-wide science competition. [link] shows the percentage breakdown of competitors from each school, and the percentage of the entire student population of the county that goes to each school. Construct a bar graph that shows the population percentage of competitors from each school.
| High School | Science competition population | Overall student population |
|---|---|---|
| Alabaster | 28.9% | 8.6% |
| Concordia | 7.6% | 23.2% |
| Genoa | 12.1% | 15.0% |
| Mocksville | 18.5% | 14.3% |
| Tynneson | 24.2% | 10.1% |
| West End | 8.7% | 28.8% |
Use the data from the David County science competition supplied in [link] . Construct a bar graph that shows the county-wide population percentage of students at each school.
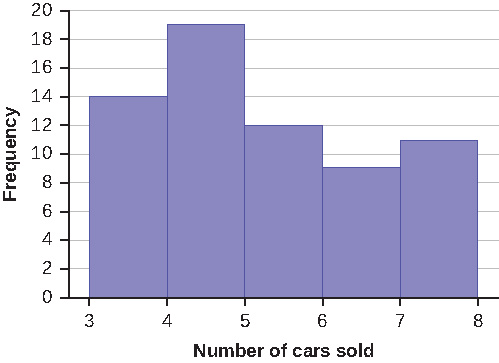
Sixty-five randomly selected car salespersons were asked the number of cars they generally sell in one week. Fourteen people answered that they generally sell three cars; nineteen generally sell four cars; twelve generally sell five cars; nine generally sell six cars; eleven generally sell seven cars. Complete the table.
| Data Value (# cars) | Frequency | Relative Frequency | Cumulative Relative Frequency |
|---|---|---|---|
What does the frequency column in [link] sum to? Why?
65
What does the relative frequency column in [link] sum to? Why?
What is the difference between relative frequency and frequency for each data value in [link] ?
The relative frequency shows the proportion of data points that have each value. The frequency tells the number of data points that have each value.
What is the difference between cumulative relative frequency and relative frequency for each data value?
To construct the histogram for the data in [link] , determine appropriate minimum and maximum x and y values and the scaling. Sketch the histogram. Label the horizontal and vertical axes with words. Include numerical scaling.

Answers will vary. One possible histogram is shown:
Construct a frequency polygon for the following:
| Pulse Rates for Women | Frequency |
|---|---|
| 60–69 | 12 |
| 70–79 | 14 |
| 80–89 | 11 |
| 90–99 | 1 |
| 100–109 | 1 |
| 110–119 | 0 |
| 120–129 | 1 |
| Actual Speed in a 30 MPH Zone | Frequency |
|---|---|
| 42–45 | 25 |
| 46–49 | 14 |
| 50–53 | 7 |
| 54–57 | 3 |
| 58–61 | 1 |
| Tar (mg) in Nonfiltered Cigarettes | Frequency |
|---|---|
| 10–13 | 1 |
| 14–17 | 0 |
| 18–21 | 15 |
| 22–25 | 7 |
| 26–29 | 2 |
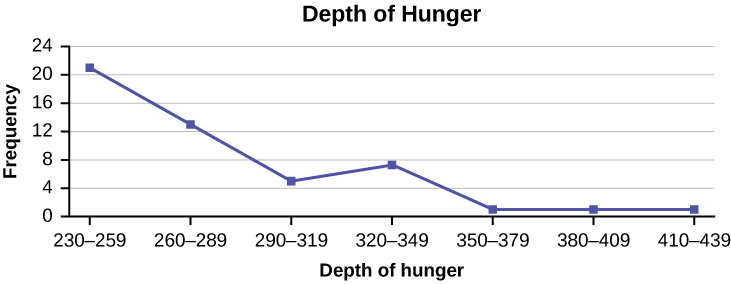
Construct a frequency polygon from the frequency distribution for the 50 highest ranked countries for depth of hunger.
| Depth of Hunger | Frequency |
|---|---|
| 230–259 | 21 |
| 260–289 | 13 |
| 290–319 | 5 |
| 320–349 | 7 |
| 350–379 | 1 |
| 380–409 | 1 |
| 410–439 | 1 |
Find the midpoint for each class. These will be graphed on the x -axis. The frequency values will be graphed on the y -axis values.
Use the two frequency tables to compare the life expectancy of men and women from 20 randomly selected countries. Include an overlayed frequency polygon and discuss the shapes of the distributions, the center, the spread, and any outliers. What can we conclude about the life expectancy of women compared to men?
| Life Expectancy at Birth – Women | Frequency |
|---|---|
| 49–55 | 3 |
| 56–62 | 3 |
| 63–69 | 1 |
| 70–76 | 3 |
| 77–83 | 8 |
| 84–90 | 2 |
| Life Expectancy at Birth – Men | Frequency |
|---|---|
| 49–55 | 3 |
| 56–62 | 3 |
| 63–69 | 1 |
| 70–76 | 1 |
| 77–83 | 7 |
| 84–90 | 5 |
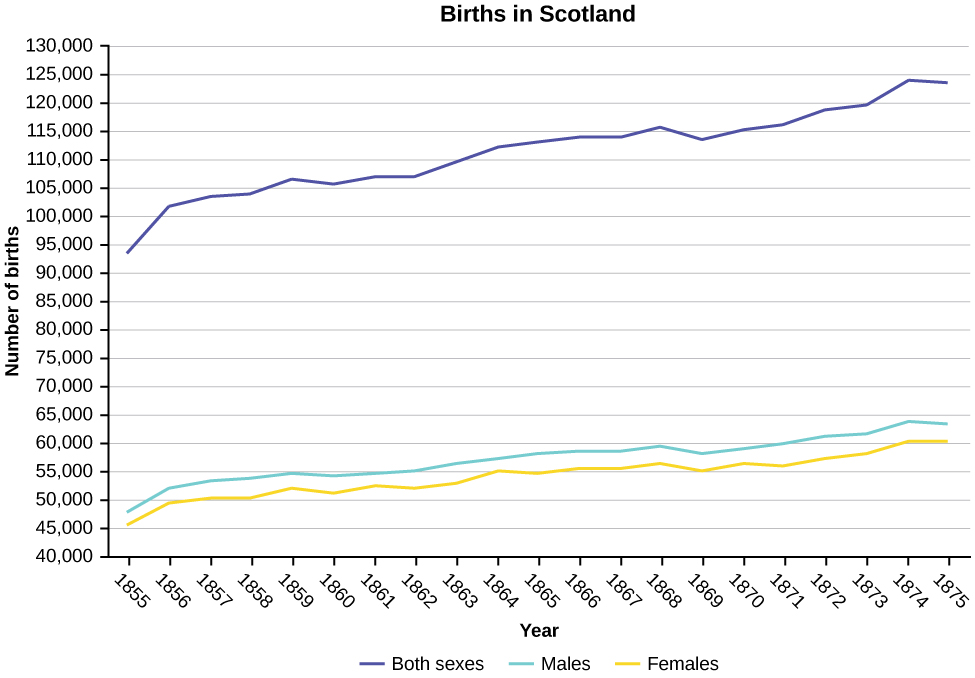
Construct a times series graph for (a) the number of male births, (b) the number of female births, and (c) the total number of births.
| Sex/Year | 1855 | 1856 | 1857 | 1858 | 1859 | 1860 | 1861 |
| Female | 45,545 | 49,582 | 50,257 | 50,324 | 51,915 | 51,220 | 52,403 |
| Male | 47,804 | 52,239 | 53,158 | 53,694 | 54,628 | 54,409 | 54,606 |
| Total | 93,349 | 101,821 | 103,415 | 104,018 | 106,543 | 105,629 | 107,009 |
| Sex/Year | 1862 | 1863 | 1864 | 1865 | 1866 | 1867 | 1868 | 1869 |
| Female | 51,812 | 53,115 | 54,959 | 54,850 | 55,307 | 55,527 | 56,292 | 55,033 |
| Male | 55,257 | 56,226 | 57,374 | 58,220 | 58,360 | 58,517 | 59,222 | 58,321 |
| Total | 107,069 | 109,341 | 112,333 | 113,070 | 113,667 | 114,044 | 115,514 | 113,354 |
| Sex/Year | 1871 | 1870 | 1872 | 1871 | 1872 | 1827 | 1874 | 1875 |
| Female | 56,099 | 56,431 | 57,472 | 56,099 | 57,472 | 58,233 | 60,109 | 60,146 |
| Male | 60,029 | 58,959 | 61,293 | 60,029 | 61,293 | 61,467 | 63,602 | 63,432 |
| Total | 116,128 | 115,390 | 118,765 | 116,128 | 118,765 | 119,700 | 123,711 | 123,578 |
The following data sets list full time police per 100,000 citizens along with homicides per 100,000 citizens for the city of Detroit, Michigan during the period from 1961 to 1973.
| Year | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 |
| Police | 260.35 | 269.8 | 272.04 | 272.96 | 272.51 | 261.34 | 268.89 |
| Homicides | 8.6 | 8.9 | 8.52 | 8.89 | 13.07 | 14.57 | 21.36 |
| Year | 1968 | 1969 | 1970 | 1971 | 1972 | 1973 |
| Police | 295.99 | 319.87 | 341.43 | 356.59 | 376.69 | 390.19 |
| Homicides | 28.03 | 31.49 | 37.39 | 46.26 | 47.24 | 52.33 |

Notification Switch
Would you like to follow the 'Introductory statistics' conversation and receive update notifications?