17.5 Equations of motion (Page 19/3)

Siyavula textbooks: grade 10 Page 1 / 3

Equations of motion

In this chapter we will look at the third way to describe motion. We have looked at describing motion in terms of graphs and words. In this section we examine equations that can be used to describe motion.

This section is about solving problems relating to uniformly accelerated motion. In other words, motion at constant acceleration.

The following are the variables that will be used in this section:

\begin{matrix} v_{i} & = & initial velocity (m \cdot s^{- 1}) at t = 0 s \\ v_{f} & = & final velocity (m \cdot s^{- 1}) at time t \\ Δ x & = & displacement (m) \\ t & = & time (s) \\ Δ t & = & time interval (s) \\ a & = & acceleration (m \cdot s^{- 1}) \end{matrix}

v_{f} = v_{i} + a t

Δ x = \frac{(v_{i} + v_{f})}{2} t

Δ x = v_{i} t + \frac{1}{2} a t^{2}

v_{f}^{2} = v_{i}^{2} + 2 a Δ x

The questions can vary a lot, but the following method for answering them will always work. Use this when attempting a question that involves motion with constant acceleration. You need any three known quantities ( $v_{i}$ , $v_{f}$ , $Δ x$ , $t$ or $a$ ) to be able to calculate the fourth one.

Read the question carefully to identify the quantities that are given. Write them down.
Identify the equation to use. Write it down!!!
Ensure that all the values are in the correct unit and fill them in your equation.
Calculate the answer and fill in its unit.

Interesting fact

Galileo Galilei of Pisa, Italy, was the first to determined the correct mathematical law foracceleration: the total distance covered, starting from rest, is proportional to the square of the time. He also concluded thatobjects retain their velocity unless a force – often friction – acts upon them, refuting the accepted Aristotelian hypothesis thatobjects "naturally" slow down and stop unless a force acts upon them. This principle was incorporated into Newton's laws of motion(1st law).

Finding the equations of motion

The following does not form part of the syllabus and can be considered additional information.

Derivation of [link]

According to the definition of acceleration:

a = \frac{Δ v}{t}

where $Δ v$ is the change in velocity, i.e. $Δ v = v_{f}$ - $v_{i}$ . Thus we have

\begin{matrix} a & = & \frac{v_{f} - v_{i}}{t} \\ v_{f} & = & v_{i} + a t \end{matrix}

Derivation of [link]

We have seen that displacement can be calculated from the area under a velocity vs. time graph. For uniformly accelerated motion the most complicated velocity vs. time graph we can have is a straight line. Look at the graph below - it represents an object with a starting velocity of $v_{i}$ , accelerating to a final velocity $v_{f}$ over a total time $t$ .

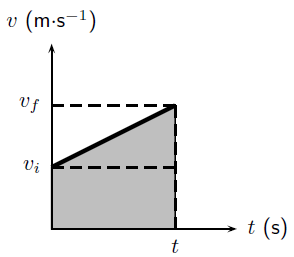
To calculate the final displacement we must calculate the area under the graph - this is just the area of the rectangle added to the area of the triangle. This portion of the graph has been shaded for clarity.

\begin{matrix} {Area}_{▵} & = & \frac{1}{2} b \times h \\ = & \frac{1}{2} t \times (v_{f} - v_{i}) \\ = & \frac{1}{2} v_{f} t - \frac{1}{2} v_{i} t \end{matrix}

\begin{matrix} {Area}_{□} & = & ℓ \times b \\ = & t \times v_{i} \\ = & v_{i} t \end{matrix}

\begin{matrix} Displacement & = & {Area}_{□} + {Area}_{▵} \\ Δ x & = & v_{i} t + \frac{1}{2} v_{f} t - \frac{1}{2} v_{i} t \\ Δ x & = & \frac{(v_{i} + v_{f})}{2} t \end{matrix}

Derivation of [link]

This equation is simply derived by eliminating the final velocity $v_{f}$ in [link] . Remembering from [link] that

v_{f} = v_{i} + a t

then [link] becomes

\begin{matrix} Δ x & = & \frac{v_{i} + v_{i} + a t}{2} t \\ = & \frac{2 v_{i} t + a t^{2}}{2} \\ Δ x & = & v_{i} t + \frac{1}{2} a t^{2} \end{matrix}

Derivation of [link]

This equation is just derived by eliminating the time variable in the above equation. From [link] we know

t = \frac{v_{f} - v_{i}}{a}

Substituting this into [link] gives

\begin{matrix} Δ x & = & v_{i} (\frac{v_{f} - v_{i}}{a}) + \frac{1}{2} a {(\frac{v_{f} - v_{i}}{a})}^{2} \\ = & \frac{v_{i} v_{f}}{a} - \frac{v_{i}^{2}}{a} + \frac{1}{2} a (\frac{v_{f}^{2} - 2 v_{i} v_{f} + v_{i}^{2}}{a^{2}}) \\ = & \frac{v_{i} v_{f}}{a} - \frac{v_{i}^{2}}{a} + \frac{v_{f}^{2}}{2 a} - \frac{v_{i} v_{f}}{a} + \frac{v_{i}^{2}}{2 a} \\ 2 a Δ x & = & - 2 v_{i}^{2} + v_{f}^{2} + v_{i}^{2} \\ v_{f}^{2} & = & v_{i}^{2} + 2 a Δ x \end{matrix}

This gives us the final velocity in terms of the initial velocity, acceleration and displacement and is independent of the time variable.

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Siyavula textbooks: grade 10 physical science [caps]. OpenStax CNX. Sep 30, 2011 Download for free at http://cnx.org/content/col11305/1.7

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Siyavula textbooks: grade 10 physical science [caps]' conversation and receive update notifications?

Ask

	8 Arts Society: Theater 8 By Jonathan Long Start Quiz
	8 Psychology MCQ 2011 1 Exam By John Gabrieli Start Exam
©flickr: Gareth	Resume Writing MCQ By Abby Sharp Start Quiz
	3 AP 03 Cellular Level of Organization MCQ By OpenStax Start Quiz
©flickr:	Arctic Ease Telemarketing Campaign Quiz By Nicole Duquette Start Quiz
	4 Microbiology Final 4 By Madison Christian Start Quiz
	6 AP Key Terms 06 The Skeletal System By OpenStax Start Key Terms
©flickr: eLife	Mycobacterial Infections (Mandell 8th Ch 251-254) By Cath Yu Start Quiz
	35 Biology 35 The Nervous System MCQ By OpenStax Start Quiz
	24 AP Key Terms 24 Metabolism Nutrition By OpenStax Start Key Terms