1. Home
  2. Siyavula textbooks: grade 10
  3. Motion in one dimension
  4. Equations of motion

17.5 Equations of motion  (Page 12/3)

<< Chapter < Page
  Siyavula textbooks: grade 10     Page 1 / 3
Chapter >> Page >

Equations of motion

In this chapter we will look at the third way to describe motion. We have looked at describing motion in terms of graphs and words. In this section we examine equations that can be used to describe motion.

This section is about solving problems relating to uniformly accelerated motion. In other words, motion at constant acceleration.

The following are the variables that will be used in this section:

v i = initial velocity ( m · s - 1 ) at t = 0 s v f = final velocity ( m · s - 1 ) at time t Δ x = displacement ( m ) t = time ( s ) Δ t = time interval ( s ) a = acceleration ( m · s - 1 )
v f = v i + a t
Δ x = ( v i + v f ) 2 t
Δ x = v i t + 1 2 a t 2
v f 2 = v i 2 + 2 a Δ x

The questions can vary a lot, but the following method for answering them will always work. Use this when attempting a question that involves motion with constant acceleration. You need any three known quantities ( v i , v f , Δ x , t or a ) to be able to calculate the fourth one.

  1. Read the question carefully to identify the quantities that are given. Write them down.
  2. Identify the equation to use. Write it down!!!
  3. Ensure that all the values are in the correct unit and fill them in your equation.
  4. Calculate the answer and fill in its unit.

Interesting fact

Galileo Galilei of Pisa, Italy, was the first to determined the correct mathematical law foracceleration: the total distance covered, starting from rest, is proportional to the square of the time. He also concluded thatobjects retain their velocity unless a force – often friction – acts upon them, refuting the accepted Aristotelian hypothesis thatobjects "naturally" slow down and stop unless a force acts upon them. This principle was incorporated into Newton's laws of motion(1st law).

Finding the equations of motion

The following does not form part of the syllabus and can be considered additional information.

Derivation of [link]

According to the definition of acceleration:

a = Δ v t

where Δ v is the change in velocity, i.e. Δ v = v f - v i . Thus we have

a = v f - v i t v f = v i + a t

Derivation of [link]

We have seen that displacement can be calculated from the area under a velocity vs. time graph. For uniformly accelerated motion the most complicated velocity vs. time graph we can have is a straight line. Look at the graph below - it represents an object with a starting velocity of v i , accelerating to a final velocity v f over a total time t .

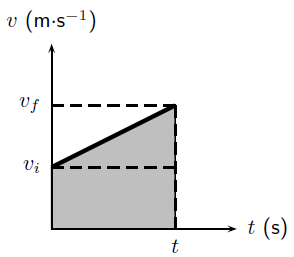
To calculate the final displacement we must calculate the area under the graph - this is just the area of the rectangle added to the area of the triangle. This portion of the graph has been shaded for clarity.

Area ▵ = 1 2 b × h = 1 2 t × ( v f - v i ) = 1 2 v f t - 1 2 v i t
Area □ = ℓ × b = t × v i = v i t
Displacement = Area □ + Area ▵ Δ x = v i t + 1 2 v f t - 1 2 v i t Δ x = ( v i + v f ) 2 t

Derivation of [link]

This equation is simply derived by eliminating the final velocity v f in [link] . Remembering from [link] that

v f = v i + a t

then [link] becomes

Δ x = v i + v i + a t 2 t = 2 v i t + a t 2 2 Δ x = v i t + 1 2 a t 2

Derivation of [link]

This equation is just derived by eliminating the time variable in the above equation. From [link] we know

t = v f - v i a

Substituting this into [link] gives

Δ x = v i ( v f - v i a ) + 1 2 a ( v f - v i a ) 2 = v i v f a - v i 2 a + 1 2 a ( v f 2 - 2 v i v f + v i 2 a 2 ) = v i v f a - v i 2 a + v f 2 2 a - v i v f a + v i 2 2 a 2 a Δ x = - 2 v i 2 + v f 2 + v i 2 v f 2 = v i 2 + 2 a Δ x

This gives us the final velocity in terms of the initial velocity, acceleration and displacement and is independent of the time variable.

Questions & Answers

A golfer on a fairway is 70 m away from the green, which sits below the level of the fairway by 20 m. If the golfer hits the ball at an angle of 40° with an initial speed of 20 m/s, how close to the green does she come?
Aislinn Reply
cm
tijani
what is titration
John Reply
what is physics
Siyaka Reply
A mouse of mass 200 g falls 100 m down a vertical mine shaft and lands at the bottom with a speed of 8.0 m/s. During its fall, how much work is done on the mouse by air resistance
Jude Reply
Can you compute that for me. Ty
Jude
what is the dimension formula of energy?
David Reply
what is viscosity?
David
what is inorganic
emma Reply
what is chemistry
Youesf Reply
what is inorganic
emma
Chemistry is a branch of science that deals with the study of matter,it composition,it structure and the changes it undergoes
Adjei
please, I'm a physics student and I need help in physics
Adjanou
chemistry could also be understood like the sexual attraction/repulsion of the male and female elements. the reaction varies depending on the energy differences of each given gender. + masculine -female.
Pedro
A ball is thrown straight up.it passes a 2.0m high window 7.50 m off the ground on it path up and takes 1.30 s to go past the window.what was the ball initial velocity
Krampah Reply
2. A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (0.20) at constant velocity by a force directed 25° above the horizontal. Calculate (a) the work of the applied force, (b) the work of friction, and (c) the total work.
Sahid Reply
you have been hired as an espert witness in a court case involving an automobile accident. the accident involved car A of mass 1500kg which crashed into stationary car B of mass 1100kg. the driver of car A applied his brakes 15 m before he skidded and crashed into car B. after the collision, car A s
Samuel Reply
can someone explain to me, an ignorant high school student, why the trend of the graph doesn't follow the fact that the higher frequency a sound wave is, the more power it is, hence, making me think the phons output would follow this general trend?
Joseph Reply
Nevermind i just realied that the graph is the phons output for a person with normal hearing and not just the phons output of the sound waves power, I should read the entire thing next time
Joseph
Follow up question, does anyone know where I can find a graph that accuretly depicts the actual relative "power" output of sound over its frequency instead of just humans hearing
Joseph
"Generation of electrical energy from sound energy | IEEE Conference Publication | IEEE Xplore" ***ieeexplore.ieee.org/document/7150687?reload=true
Ryan
what's motion
Maurice Reply
what are the types of wave
Maurice
answer
Magreth
progressive wave
Magreth
hello friend how are you
Muhammad Reply
fine, how about you?
Mohammed
hi
Mujahid
A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
yasuo Reply
Who can show me the full solution in this problem?
Reofrir Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Siyavula textbooks: grade 10 physical science [caps]. OpenStax CNX. Sep 30, 2011 Download for free at http://cnx.org/content/col11305/1.7
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Siyavula textbooks: grade 10 physical science [caps]' conversation and receive update notifications?

Ask