16.5 Telescopes  (Page 2/4)

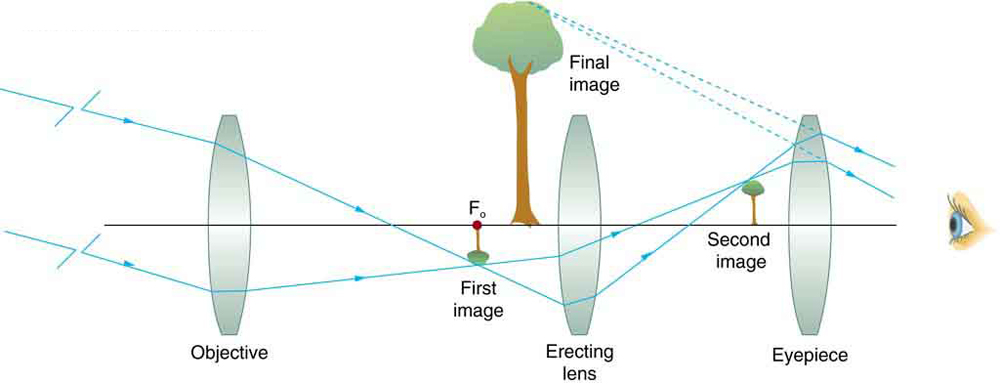
The image in most telescopes is inverted, which is unimportant for observing the stars but a real problem for other applications, such as telescopes on ships or telescopic gun sights. If an upright image is needed, Galileo’s arrangement in [link] (a) can be used. But a more common arrangement is to use a third convex lens as an eyepiece, increasing the distance between the first two and inverting the image once again as seen in [link] .

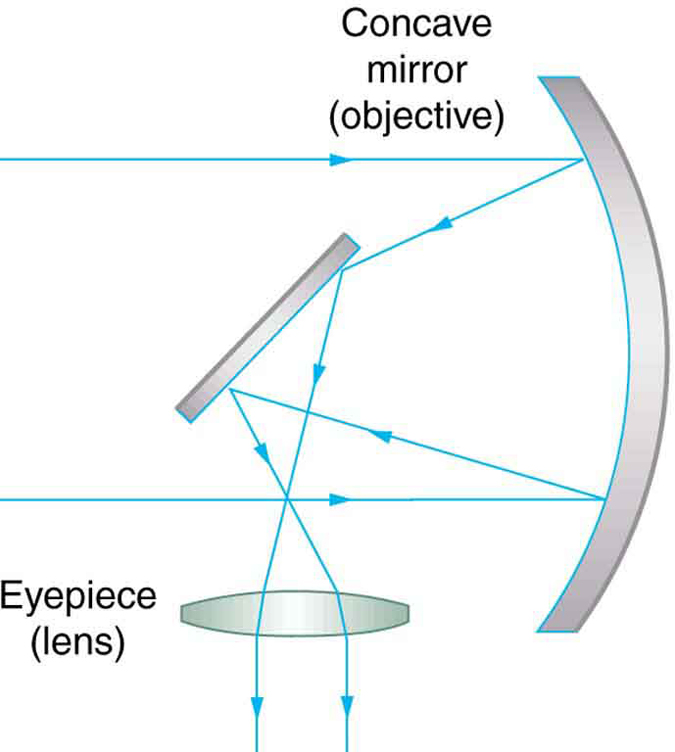
A telescope can also be made with a concave mirror as its first element or objective, since a concave mirror acts like a convex lens as seen in [link] . Flat mirrors are often employed in optical instruments to make them more compact or to send light to cameras and other sensing devices. There are many advantages to using mirrors rather than lenses for telescope objectives. Mirrors can be constructed much larger than lenses and can, thus, gather large amounts of light, as needed to view distant galaxies, for example. Large and relatively flat mirrors have very long focal lengths, so that great angular magnification is possible.

Telescopes, like microscopes, can utilize a range of frequencies from the electromagnetic spectrum. [link] (a) shows the Australia Telescope Compact Array, which uses six 22-m antennas for mapping the southern skies using radio waves. [link] (b) shows the focusing of x rays on the Chandra X-ray Observatory—a satellite orbiting earth since 1999 and looking at high temperature events as exploding stars, quasars, and black holes. X rays, with much more energy and shorter wavelengths than RF and light, are mainly absorbed and not reflected when incident perpendicular to the medium. But they can be reflected when incident at small glancing angles, much like a rock will skip on a lake if thrown at a small angle. The mirrors for the Chandra consist of a long barrelled pathway and 4 pairs of mirrors to focus the rays at a point 10 meters away from the entrance. The mirrors are extremely smooth and consist of a glass ceramic base with a thin coating of metal (iridium). Four pairs of precision manufactured mirrors are exquisitely shaped and aligned so that x rays ricochet off the mirrors like bullets off a wall, focusing on a spot.

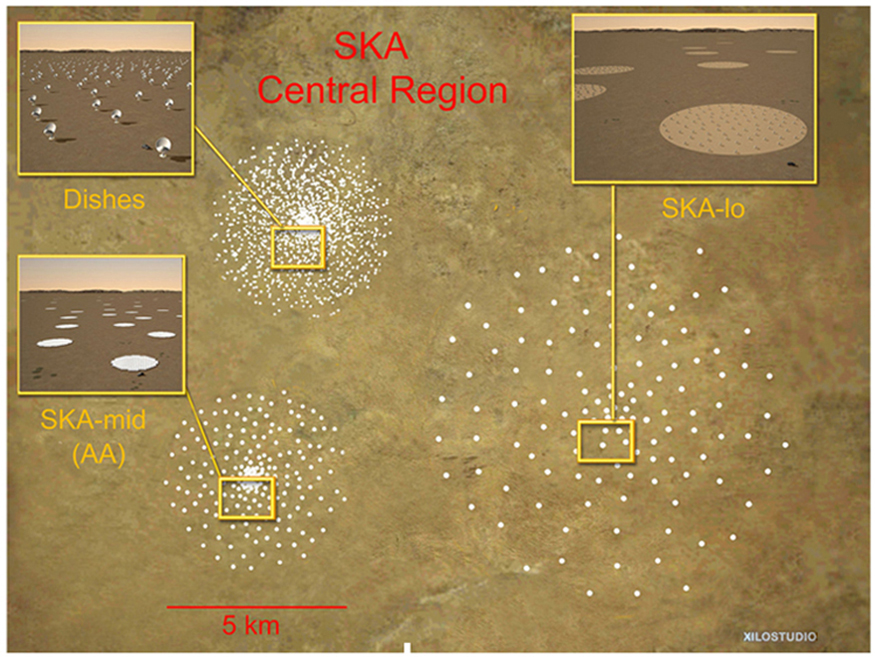
A current exciting development is a collaborative effort involving 17 countries to construct a Square Kilometre Array (SKA) of telescopes capable of covering from 80 MHz to 2 GHz. The initial stage of the project is the construction of the Australian Square Kilometre Array Pathfinder in Western Australia (see [link] ). The project will use cutting-edge technologies such as adaptive optics    in which the lens or mirror is constructed from lots of carefully aligned tiny lenses and mirrors that can be manipulated using computers. A range of rapidly changing distortions can be minimized by deforming or tilting the tiny lenses and mirrors. The use of adaptive optics in vision correction is a current area of research.

Section summary

• Simple telescopes can be made with two lenses. They are used for viewing objects at large distances and utilize the entire range of the electromagnetic spectrum.
• The angular magnification M for a telescope is given by
  $M=\frac{\theta \prime }{\theta }=-\frac{f_{\text{o}}}{f_{\text{e}}}\text{,}$
  where $\theta$ is the angle subtended by an object viewed by the unaided eye, $\theta \prime$ is the angle subtended by a magnified image, and $f_{\text{o}}$ and $f_{\text{e}}$ are the focal lengths of the objective and the eyepiece.

Conceptual questions

Problem exercises

Unless otherwise stated, the lens-to-retina distance is 2.00 cm.