16.4 Electric generators  (Page 8/6)

Electric generators induce an emf by rotating a coil in a magnetic field, as briefly discussed in Induced Emf and Magnetic Flux . We will now explore generators in more detail. Consider the following example.

Calculating the emf induced in a generator coil

The generator coil shown in [link] is rotated through one-fourth of a revolution (from $\theta =\mathrm{0º}$ to $\theta =\text{90º}$ ) in 15.0 ms. The 200-turn circular coil has a 5.00 cm radius and is in a uniform 1.25 T magnetic field. What is the average emf induced?

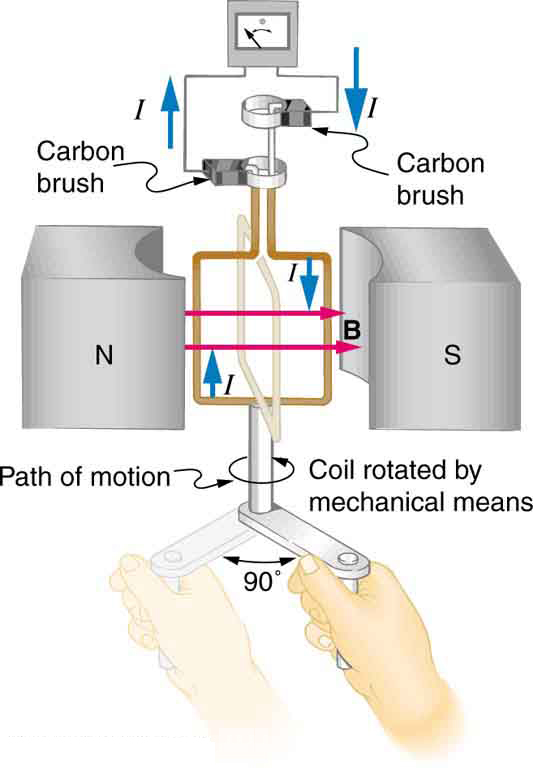
Strategy

We use Faraday’s law of induction to find the average emf induced over a time $\mathrm{\Delta }t$ :

$\text{emf}=-N\frac{\mathrm{\Delta }\Phi }{\mathrm{\Delta }t}\text{.}$

We know that $N=\text{200}$ and $\mathrm{\Delta }t=\text{15}\text{.}0\text{ms}$ , and so we must determine the change in flux $\mathrm{\Delta }\Phi$ to find emf.

Solution

Since the area of the loop and the magnetic field strength are constant, we see that

$\mathrm{\Delta }\Phi =\mathrm{\Delta }(\text{BA}\text{cos}\theta )=\text{AB}\mathrm{\Delta }(\text{cos}\theta )\text{.}$

Now, $\mathrm{\Delta }(\text{cos}\theta )=-1\text{.}0$ , since it was given that $\theta$ goes from $\text{0º}$ to $\text{90º}$ . Thus $\mathrm{\Delta }\Phi =-\text{AB}$ , and

$\text{emf}=N\frac{\text{AB}}{\mathrm{\Delta }t}.$

The area of the loop is $A={\mathrm{\pi r}}^2=(3\text{.}\text{14}\text{.}\text{.}\text{.})(0\text{.}\text{0500}\text{m}{)}^2=7\text{.}\text{85}\times {\text{10}}^{-3}{\text{m}}^2$ . Entering this value gives

$\text{emf}=\text{200}\frac{(7\text{.}\text{85}\times {\text{10}}^{-3}{\text{m}}^2)(1\text{.}\text{25}\text{T})}{\text{15}\text{.}0\times {\text{10}}^{-3}\text{s}}=\text{131}\text{V.}$

Discussion

This is a practical average value, similar to the 120 V used in household power.

The emf calculated in [link] is the average over one-fourth of a revolution. What is the emf at any given instant? It varies with the angle between the magnetic field and a perpendicular to the coil. We can get an expression for emf as a function of time by considering the motional emf on a rotating rectangular coil of width $w$ and height $\ell$ in a uniform magnetic field, as illustrated in [link] .

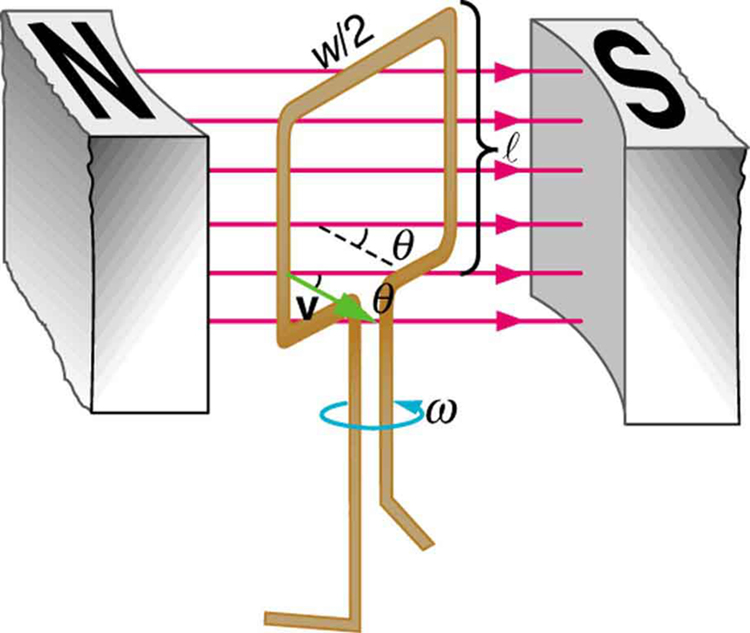
Charges in the wires of the loop experience the magnetic force, because they are moving in a magnetic field. Charges in the vertical wires experience forces parallel to the wire, causing currents. But those in the top and bottom segments feel a force perpendicular to the wire, which does not cause a current. We can thus find the induced emf by considering only the side wires. Motional emf is given to be $\text{emf}=\mathrm{B\ell v}$ , where the velocity v is perpendicular to the magnetic field $B$ . Here the velocity is at an angle $\theta$ with $B$ , so that its component perpendicular to $B$ is $v\text{sin}\theta$ (see [link] ). Thus in this case the emf induced on each side is $\text{emf}=\mathrm{B\ell v}\text{sin}\theta$ , and they are in the same direction. The total emf around the loop is then

This expression is valid, but it does not give emf as a function of time. To find the time dependence of emf, we assume the coil rotates at a constant angular velocity $\omega$ . The angle $\theta$ is related to angular velocity by $\theta =\mathrm{\omega t}$ , so that

Now, linear velocity $v$ is related to angular velocity $\omega$ by $v=\mathrm{r\omega }$ . Here $r=w/2$ , so that $v=(w/2)\omega$ , and