| << Chapter < Page | Chapter >> Page > |
In the discussion of vector addition we saw that a number of vectors acting together can be combined to give a single vector (the resultant). Inmuch the same way a single vector can be broken down into a number of vectors which when added give that original vector. These vectors which sum to the original are called components of the original vector. The process of breaking a vector into its components is called resolving into components .
While summing a given set of vectors gives just one answer (the resultant), a single vector can be resolved into infinitely many setsof components. In the diagrams below the same black vector is resolved into different pairs of components. These components are shown as dashed lines. When added together the dashed vectors give the original black vector(i.e. the original vector is the resultant of its components).
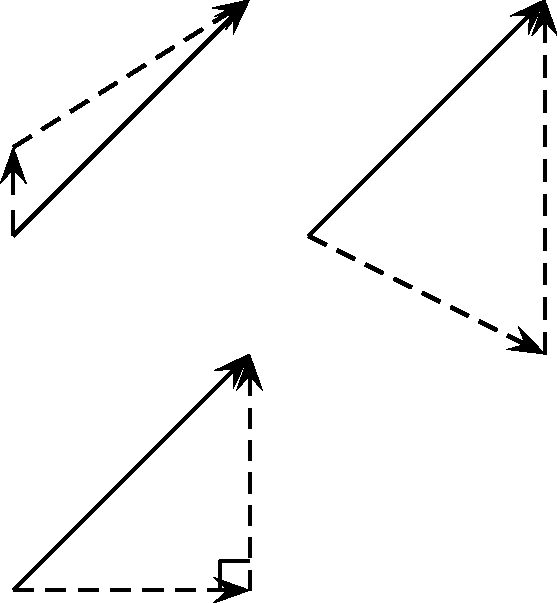
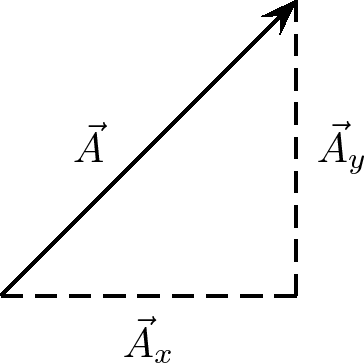
In practice it is most useful to resolve a vector into components which are at right angles to one another, usually horizontal and vertical.
Any vector can be resolved into a horizontal and a vertical component. If is a vector, then the horizontal component of is and the vertical component is .
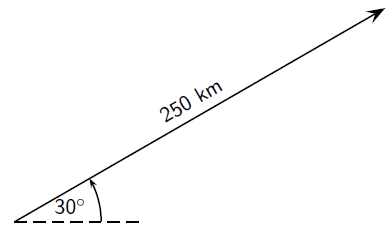
A motorist undergoes a displacement of 250 km in a direction north of east. Resolve this displacement into components in the directions north ( ) and east ( ).
Next we resolve the displacement into its components north and east. Since these directions are perpendicular to one another, thecomponents form a right-angled triangle with the original displacement as its hypotenuse.
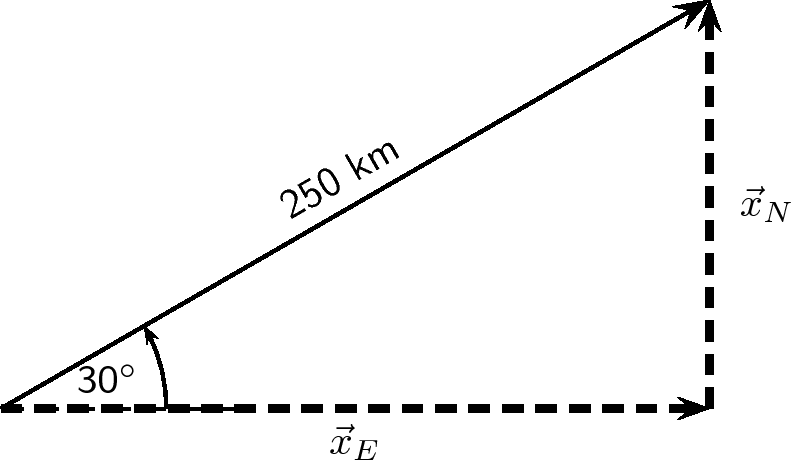
Notice how the two components acting together give the original vector as their resultant.
Now we can use trigonometry to calculate the magnitudes of the components of the original displacement:
and
Remember and are the magnitudes of the components – they are in the directions north and east respectively.
Components can also be used to find the resultant of vectors. This technique can be applied to both graphical and algebraic methods of finding the resultant. The method is simple: make a rough sketch of the problem, find the horizontal and vertical components of each vector, find the sum of all horizontal components and the sum of all the vertical components and then use them to find the resultant.
Consider the two vectors, and , in [link] , together with their resultant, .
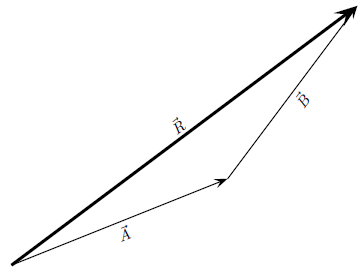
Each vector in [link] can be broken down into one component in the -direction (horizontal) and one in the -direction (vertical). These components are two vectors which when added give you the original vector as the resultant. This is shown in [link] where we can see that:
In summary, addition of the components of the two original vectors gives the component of the resultant. The same applies to the components. So if we just added all the components together we would get the same answer! This is another importantproperty of vectors.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 physical science [caps]' conversation and receive update notifications?