15.3 Sound intensity and sound level  (Page 20/7)

In a quiet forest, you can sometimes hear a single leaf fall to the ground. After settling into bed, you may hear your blood pulsing through your ears. But when a passing motorist has his stereo turned up, you cannot even hear what the person next to you in your car is saying. We are all very familiar with the loudness of sounds and aware that they are related to how energetically the source is vibrating. In cartoons depicting a screaming person (or an animal making a loud noise), the cartoonist often shows an open mouth with a vibrating uvula, the hanging tissue at the back of the mouth, to suggest a loud sound coming from the throat [link] . High noise exposure is hazardous to hearing, and it is common for musicians to have hearing losses that are sufficiently severe that they interfere with the musicians’ abilities to perform. The relevant physical quantity is sound intensity, a concept that is valid for all sounds whether or not they are in the audible range.

Intensity is defined to be the power per unit area carried by a wave. Power is the rate at which energy is transferred by the wave. In equation form, intensity     $I$ is

where $P$ is the power through an area $A$ . The SI unit for $I$ is ${\mathrm{W/m}}^2$ . The intensity of a sound wave is related to its amplitude squared by the following relationship:

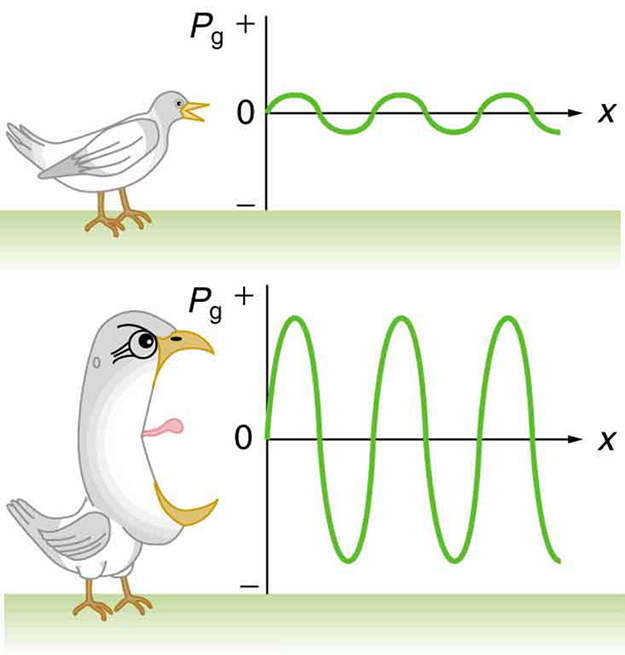
Here $\mathrm{\Delta }p$ is the pressure variation or pressure amplitude (half the difference between the maximum and minimum pressure in the sound wave) in units of pascals (Pa) or ${\mathrm{N/m}}^2$ . (We are using a lower case $p$ for pressure to distinguish it from power, denoted by $P$ above.) The energy (as kinetic energy $\frac{{\mathrm{mv}}^2}{2}$ ) of an oscillating element of air due to a traveling sound wave is proportional to its amplitude squared. In this equation, $\rho$ is the density of the material in which the sound wave travels, in units of ${\mathrm{kg/m}}^3$ , and $v_{\mathrm{w}}$ is the speed of sound in the medium, in units of m/s. The pressure variation is proportional to the amplitude of the oscillation, and so $I$ varies as $(\mathrm{\Delta }p{)}^2$ ( [link] ). This relationship is consistent with the fact that the sound wave is produced by some vibration; the greater its pressure amplitude, the more the air is compressed in the sound it creates.

Sound intensity levels are quoted in decibels (dB) much more often than sound intensities in watts per meter squared. Decibels are the unit of choice in the scientific literature as well as in the popular media. The reasons for this choice of units are related to how we perceive sounds. How our ears perceive sound can be more accurately described by the logarithm of the intensity rather than directly to the intensity. The sound intensity level     $\beta$ in decibels of a sound having an intensity $I$ in watts per meter squared is defined to be