14.7 Electromotive force: terminal voltage  (Page 4/12)

Discussion for (a)

The terminal voltage here is only slightly lower than the emf, implying that $\text{10}\text{.}0\Omega$ is a light load for this particular battery.

Solution for (b)

Similarly, with $R_{\text{load}}=0\text{.}\text{500}\Omega$ , the current is

The terminal voltage is now

Discussion for (b)

This terminal voltage exhibits a more significant reduction compared with emf, implying $0\text{.}\text{500}\Omega$ is a heavy load for this battery.

Solution for (c)

The power dissipated by the $0\text{.}\text{500 - Ω}$ load can be found using the formula $P=I^{2}R$ . Entering the known values gives

Discussion for (c)

Note that this power can also be obtained using the expressions $\frac{V^2}{R}$ or $\text{IV}$ , where $V$ is the terminal voltage (10.0 V in this case).

Solution for (d)

Here the internal resistance has increased, perhaps due to the depletion of the battery, to the point where it is as great as the load resistance. As before, we first find the current by entering the known values into the expression, yielding

Now the terminal voltage is

and the power dissipated by the load is

Discussion for (d)

We see that the increased internal resistance has significantly decreased terminal voltage, current, and power delivered to a load.

Battery testers, such as those in [link] , use small load resistors to intentionally draw current to determine whether the terminal voltage drops below an acceptable level. They really test the internal resistance of the battery. If internal resistance is high, the battery is weak, as evidenced by its low terminal voltage.

Some batteries can be recharged by passing a current through them in the direction opposite to the current they supply to a resistance. This is done routinely in cars and batteries for small electrical appliances and electronic devices, and is represented pictorially in [link] . The voltage output of the battery charger must be greater than the emf of the battery to reverse current through it. This will cause the terminal voltage of the battery to be greater than the emf, since $V=\text{emf}-\text{Ir}$ , and $I$ is now negative.

Multiple voltage sources

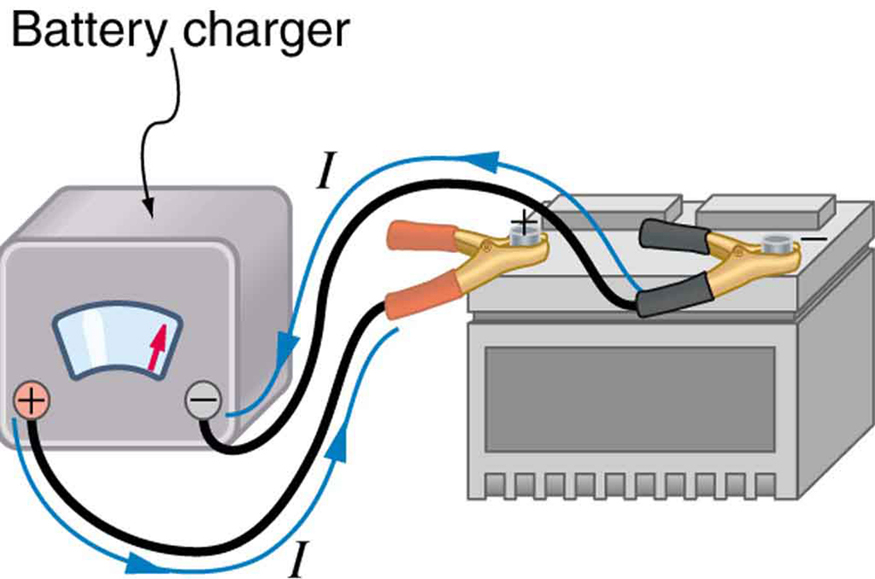
There are two voltage sources when a battery charger is used. Voltage sources connected in series are relatively simple. When voltage sources are in series, their internal resistances add and their emfs add algebraically. (See [link] .) Series connections of voltage sources are common—for example, in flashlights, toys, and other appliances. Usually, the cells are in series in order to produce a larger total emf.