13.8 Outliers  (Page 2/3)

Numerical identification of outliers: calculating $s$ And finding outliers manually

If you do not have the function LinRegTTest, then you can calculate the outlier in the first example by doing the following.

First, square each $|y-\hat{y}|$ (See the TABLE above):

The squares are

• ${35}^2$
• ${17}^2$
• ${16}^2$
• $6^2$
• ${19}^2$
• $9^2$
• $3^2$
• $1^2$
• ${10}^2$
• $9^2$
• $1^2$

Then, add (sum) all the $|y-\hat{y}|$ squared terms using the formula

$\stackrel{11}{\underset{\text{i = 1}}{\Sigma }}\left(\right|y_i-{\hat{y}}_i|{)}^2=\stackrel{11}{\underset{\text{i = 1}}{\Sigma }}{{\epsilon }_i}^2$ (Recall that $y_i-{\hat{y}}_i={\epsilon }_i$ .)

$={35}^2+{17}^2+{16}^2+6^2+{19}^2+9^2+3^2+1^2+{10}^2+9^2+1^2$

$=2440=$ SSE . The result, SSE is the Sum of Squared Errors.

Next, calculate $s$ , the standard deviation of all the $y-\hat{y}=\epsilon$ values where $n$ = the total number of data points.

The calculation is $s=\sqrt{\frac{\text{SSE}}{n-2}}$

For the third exam/final exam problem, $s=\sqrt{\frac{2440}{11-2}}=16.47$

Next, multiply $s$ by $1.9$ :
$\left(1.9\right)\cdot \left(16.47\right)=31.29$
31.29 is almost 2 standard deviations away from the mean of the $y-\hat{y}$ values.

If we were to measure the vertical distance from any data point to the corresponding point on the line of best fit and that distance is at least $1.9s$ , then we would consider the data point to be "too far" from the line of best fit. We call that point a potential outlier .

For the example, if any of the $|y-\hat{y}|$ values are at least 31.29, the corresponding $(x,y)$ data point is a potential outlier.

For the third exam/final exam problem, all the $|y-\hat{y}|$ 's are less than 31.29 except for the first one which is 35.

$35>31.29$ That is, $|y-\hat{y}|\ge \left(1.9\right)\cdot \left(s\right)$

The point which corresponds to $|y-\hat{y}|=35$ is $(65,175)$ . Therefore, the data point $(65,175)$ is a potential outlier. For this example, we will delete it. (Remember, we do not always delete an outlier.)

The next step is to compute a new best-fit line using the 10 remaining points. The new line of best fit and the correlation coefficient are:

$\hat{y}=-355.19+\text{7.39}x$ and $r=0.9121$

( From The Consumer Price Indexes Web site ) The Consumer Price Index (CPI) measures the average change over time in the prices paid by urban consumers for consumer goods and services. The CPI affects nearly all Americans because of the many waysit is used. One of its biggest uses is as a measure of inflation. By providing information about price changes in the Nation's economy to government, business, and labor, the CPI helps themto make economic decisions. The President, Congress, and the Federal Reserve Board use the CPI's trends to formulate monetary and fiscal policies. In the following table, $x$ is the year and $y$ is the CPI.

• Make a scatterplot of the data.
• Calculate the least squares line. Write the equation in the form $\hat{y}=a+\text{b}x$ .
• Draw the line on the scatterplot.
• Find the correlation coefficient. Is it significant?
• What is the average CPI for the year 1990?

• Scatter plot and line of best fit.
• $\hat{y}=-3204+\text{1.662}x$ is the equation of the line of best fit.
• $r=0.8694$
• The number of data points is $n=14$ . Use the 95% Critical Values of the Sample Correlation Coefficient table at the end of Chapter 12. $n-2=12$ . The corresponding critical value is 0.532. Since $0.8694>0.532$ , $r$ is significant.
• $\hat{y}=-3204+1.662\left(1990\right)=103.4$ CPI
• Using the calculator LinRegTTest, we find that s = 25.4 ; graphing the lines Y2=-3204+1.662X-2(25.4) and Y3=-3204+1.662X+2(25.4) shows that no data values are outside those lines, identifying no outliers. (Note that the year 1999 was very close to the upper line, but still inside it.)

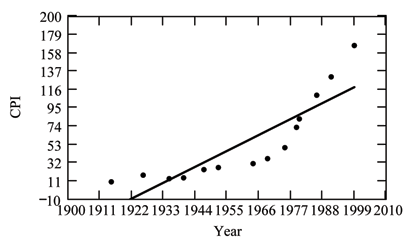
If you are interested in seeing more years of data, visit the Bureau of Labor Statistics CPI website ftp://ftp.bls.gov/pub/special.requests/cpi/cpiai.txt ; our data is taken from the column entitled "Annual Avg." (third column from the right). For example you could add more current years of data. Try adding the more recent years 2004 : CPI=188.9, 2008 : CPI=215.3 and 2011: CPI=224.9. See how it affects the model. (Check: $\hat{y}=-4436+\text{2.295}x$ . $\mathrm{r\; =\; 0.9018}$ . Is $r$ significant? Is the fit better with the addition of the new points?)

**With contributions from Roberta Bloom