13.7 Statistical interpretation of entropy and the second law of  (Page 3/8)

The most likely conditions (or macrostates) for a gas are those we see all the time—a random distribution of atoms in space with a Maxwell-Boltzmann distribution of speeds in random directions, as predicted by kinetic theory. This is the most disorderly and least structured condition we can imagine. In contrast, one type of very orderly and structured macrostate has all of the atoms in one corner of a container with identical velocities. There are very few ways to accomplish this (very few microstates corresponding to it), and so it is exceedingly unlikely ever to occur. (See [link] (b).) Indeed, it is so unlikely that we have a law saying that it is impossible, which has never been observed to be violated—the second law of thermodynamics.

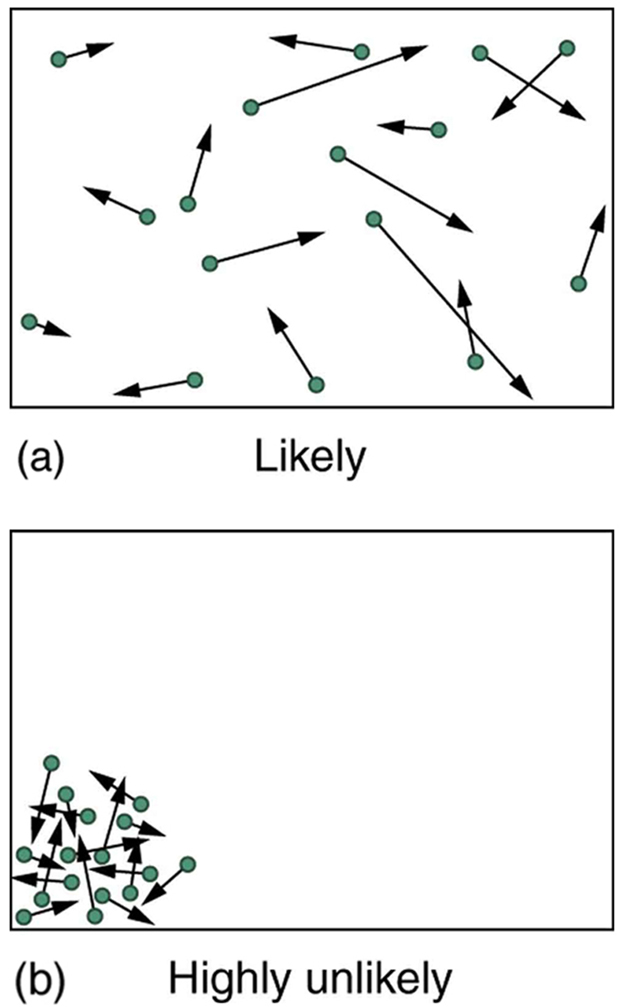
The disordered condition is one of high entropy, and the ordered one has low entropy. With a transfer of energy from another system, we could force all of the atoms into one corner and have a local decrease in entropy, but at the cost of an overall increase in entropy of the universe. If the atoms start out in one corner, they will quickly disperse and become uniformly distributed and will never return to the orderly original state ( [link] (b)). Entropy will increase. With such a large sample of atoms, it is possible—but unimaginably unlikely—for entropy to decrease. Disorder is vastly more likely than order.

The arguments that disorder and high entropy are the most probable states are quite convincing. The great Austrian physicist Ludwig Boltzmann (1844–1906)—who, along with Maxwell, made so many contributions to kinetic theory—proved that the entropy of a system in a given state (a macrostate) can be written as

where $k=1\text{.}\text{38}\times {\text{10}}^{-\text{23}}\text{J/K}$ is Boltzmann’s constant, and $\text{ln}W$ is the natural logarithm of the number of microstates $W$ corresponding to the given macrostate. $W$ is proportional to the probability that the macrostate will occur. Thus entropy is directly related to the probability of a state—the more likely the state, the greater its entropy. Boltzmann proved that this expression for $S$ is equivalent to the definition $\mathrm{\Delta }S=Q/T$ , which we have used extensively.

Thus the second law of thermodynamics is explained on a very basic level: entropy either remains the same or increases in every process. This phenomenon is due to the extraordinarily small probability of a decrease, based on the extraordinarily larger number of microstates in systems with greater entropy. Entropy can decrease, but for any macroscopic system, this outcome is so unlikely that it will never be observed.