13.4 Total internal reflection  (Page 20/3)

Total internal reflection and fibre optics

Total internal reflection

Investigation : total internal reflection

Work in groups of four. Each group will need a raybox (or torch) with slit, triangular glass prism and protractor. If you do not have a raybox, use a torch and stick two pieces of tape over the lens so that only a thin beam of light is visible.

Aim:

To investigate total internal reflection.

Method:

1. Place the raybox next to the glass block so that the light shines right through without any refraction. See "Position 1" in diagram.

   

2. Move the raybox such that the light is refracted by the glass. See "Position 2".

   

3. Move the raybox further and observe what happens.

   

4. Move the raybox until the refracted ray seems to disappear. See "Position 4". The angle of the incident light is called the critical angle.

   

5. Move the raybox further and observe what happens. See "Position 5". The light shines back into the glass block. This is called total internal reflection.

   

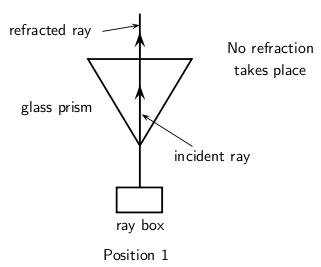
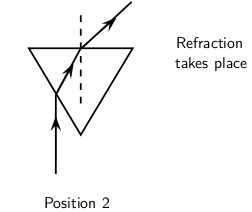
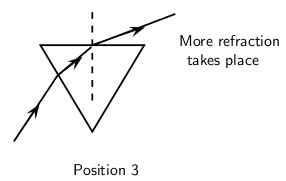
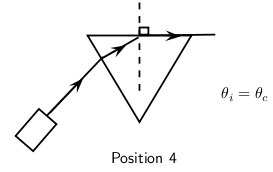
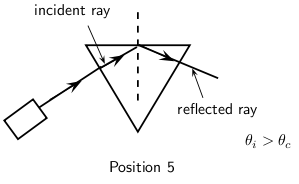
When we increase the angle of incidence, we reach a point where the angle of refraction is 90 ${}^{\circ }$ and the refracted ray runs along the surface of the medium. This angle of incidence is called the critical angle.

Critical Angle

The critical angle is the angle of incidence where the angle of reflection is 90 ${}^{\circ }$ . The light must shine from a dense to a less dense medium.

If the angle of incidence is bigger than this critical angle, the refracted ray will not emerge from the medium, but will be reflected back into the medium. This is called total internal reflection.

Total internal reflection takes place when

• light shines from an optically denser medium to an optically less dense medium.
• the angle of incidence is greater than the critical angle.

Total Internal Reflection

Total internal reflection takes place when light is reflected back into the medium because the angle of incidence is greater than the critical angle.

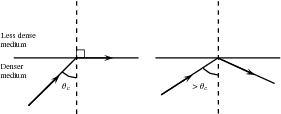
Each medium has its own unique critical angle. For example, the critical angle for glass is 42 ${}^{\circ }$ , and that of water is 48,8 ${}^{\circ }$ . We can calculate the critical angle for any medium.

Calculating the critical angle

Now we shall learn how to derive the value of the critical angle for two given media. The process is fairly simple and involves just the use of Snell's Law that we have already studied. To recap, Snell's Law states:

where $n_1$ is the refractive index of material 1, $n_2$ is the refractive index of material 2, ${\theta }_1$ is the angle of incidence and ${\theta }_2$ is the angle of refraction. For total internal reflection we know that the angle of incidence is the critical angle. So,

However, we also know that the angle of refraction at the critical angle is 90 ${}^{\circ }$ . So we have:

We can then write Snell's Law as:

Solving for ${\theta }_c$ gives: