| << Chapter < Page | Chapter >> Page > |
Solution for (a)
1. Identify the knowns and what we want to solve for. We know that ; ; ( is negative because it is in a direction opposite to velocity). We take to be 0. We are looking for displacement , or .
2. Identify the equation that will help up solve the problem. The best equation to use is
This equation is best because it includes only one unknown, . We know the values of all the other variables in this equation. (There are other equations that would allow us to solve for , but they require us to know the stopping time, , which we do not know. We could use them but it would entail additional calculations.)
3. Rearrange the equation to solve for .
4. Enter known values.
Thus,
Solution for (b)
This part can be solved in exactly the same manner as Part A. The only difference is that the deceleration is . The result is
Solution for (c)
Once the driver reacts, the stopping distance is the same as it is in Parts A and B for dry and wet concrete. So to answer this question, we need to calculate how far the car travels during the reaction time, and then add that to the stopping time. It is reasonable to assume that the velocity remains constant during the driver’s reaction time.
1. Identify the knowns and what we want to solve for. We know that ; ; . We take to be 0. We are looking for .
2. Identify the best equation to use.
works well because the only unknown value is , which is what we want to solve for.
3. Plug in the knowns to solve the equation.
This means the car travels 15.0 m while the driver reacts, making the total displacements in the two cases of dry and wet concrete 15.0 m greater than if he reacted instantly.
4. Add the displacement during the reaction time to the displacement when braking.
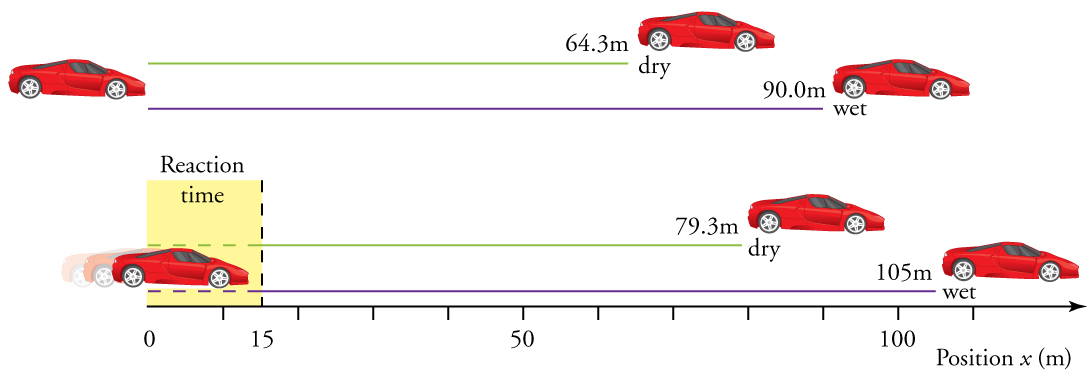
Discussion
The displacements found in this example seem reasonable for stopping a fast-moving car. It should take longer to stop a car on wet rather than dry pavement. It is interesting that reaction time adds significantly to the displacements. But more important is the general approach to solving problems. We identify the knowns and the quantities to be determined and then find an appropriate equation. There is often more than one way to solve a problem. The various parts of this example can in fact be solved by other methods, but the solutions presented above are the shortest.

Notification Switch
Would you like to follow the 'Physics 105: adventures in physics' conversation and receive update notifications?