13.3 Spectroscopic and magnetic properties of coordination compounds  (Page 2/17)

In octahedral complexes, the lobes in two of the five d orbitals, the $d_{z^2}$ and $d_{x^2\text{−}{y}^2}$ orbitals, point toward the ligands ( [link] ). These two orbitals are called the e _g orbitals    (the symbol actually refers to the symmetry of the orbitals, but we will use it as a convenient name for these two orbitals in an octahedral complex). The other three orbitals, the d _xy , d _xz , and d _yz orbitals, have lobes that point between the ligands and are called the t _{2 g} orbitals    (again, the symbol really refers to the symmetry of the orbitals). As six ligands approach the metal ion along the axes of the octahedron, their point charges repel the electrons in the d orbitals of the metal ion. However, the repulsions between the electrons in the e _g orbitals (the $d_{z^2}$ and $d_{x^2\text{−}{y}^2}$ orbitals) and the ligands are greater than the repulsions between the electrons in the t _{2 g} orbitals (the d _zy , d _xz , and d _yz orbitals) and the ligands. This is because the lobes of the e _g orbitals point directly at the ligands, whereas the lobes of the t _{2 g} orbitals point between them. Thus, electrons in the e _g orbitals of the metal ion in an octahedral complex have higher potential energies than those of electrons in the t _{2 g} orbitals. The difference in energy may be represented as shown in [link] .

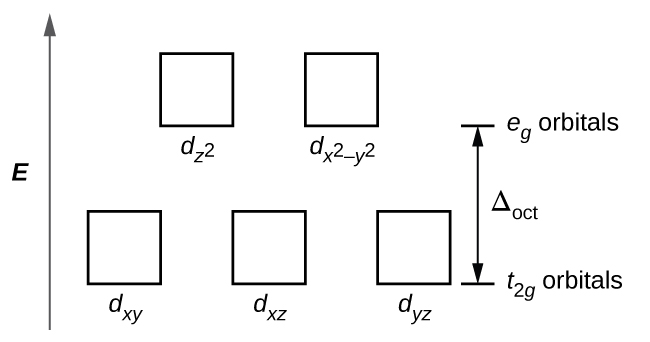
The difference in energy between the e _g and the t _{2 g} orbitals is called the crystal field splitting and is symbolized by Δoct , where oct stands for octahedral.

The magnitude of Δ _oct depends on many factors, including the nature of the six ligands located around the central metal ion, the charge on the metal, and whether the metal is using 3 d , 4 d , or 5 d orbitals. Different ligands produce different crystal field splittings. The increasing crystal field splitting produced by ligands is expressed in the spectrochemical series    , a short version of which is given here:

In this series, ligands on the left cause small crystal field splittings and are weak-field ligands , whereas those on the right cause larger splittings and are strong-field ligands . Thus, the Δ _oct value for an octahedral complex with iodide ligands (I ⁻ ) is much smaller than the Δ _oct value for the same metal with cyanide ligands (CN ⁻ ).

Electrons in the d orbitals follow the aufbau (“filling up”) principle, which says that the orbitals will be filled to give the lowest total energy, just as in main group chemistry. When two electrons occupy the same orbital, the like charges repel each other. The energy needed to pair up two electrons in a single orbital is called the pairing energy (P)    . Electrons will always singly occupy each orbital in a degenerate set before pairing. P is similar in magnitude to Δ _oct . When electrons fill the d orbitals, the relative magnitudes of Δ _oct and P determine which orbitals will be occupied.