| << Chapter < Page | Chapter >> Page > |

If we are interested in how heat transfer is converted into doing work, then the conservation of energy principle is important. The first law of thermodynamics applies the conservation of energy principle to systems where heat transfer and doing work are the methods of transferring energy into and out of the system. The first law of thermodynamics states that the change in internal energy of a system equals the net heat transfer into the system minus the net work done by the system. In equation form, the first law of thermodynamics is
Here is the change in internal energy of the system. is the net heat transferred into the system —that is, is the sum of all heat transfer into and out of the system. is the net work done by the system —that is, is the sum of all work done on or by the system. We use the following sign conventions: if is positive, then there is a net heat transfer into the system; if is positive, then there is net work done by the system. So positive adds energy to the system and positive takes energy from the system. Thus . Note also that if more heat transfer into the system occurs than work done, the difference is stored as internal energy. Heat engines are a good example of this—heat transfer into them takes place so that they can do work. (See [link] .) We will now examine , , and further.
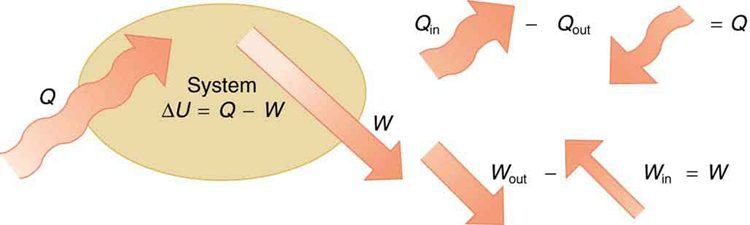
The first law of thermodynamics is actually the law of conservation of energy stated in a form most useful in thermodynamics. The first law gives the relationship between heat transfer, work done, and the change in internal energy of a system.
Heat transfer ( ) and doing work ( ) are the two everyday means of bringing energy into or taking energy out of a system. The processes are quite different. Heat transfer, a less organized process, is driven by temperature differences. Work, a quite organized process, involves a macroscopic force exerted through a distance. Nevertheless, heat and work can produce identical results. For example, both can cause a temperature increase. Heat transfer into a system, such as when the Sun warms the air in a bicycle tire, can increase its temperature, and so can work done on the system, as when the bicyclist pumps air into the tire. Once the temperature increase has occurred, it is impossible to tell whether it was caused by heat transfer or by doing work. This uncertainty is an important point. Heat transfer and work are both energy in transit—neither is stored as such in a system. However, both can change the internal energy of a system. Internal energy is a form of energy completely different from either heat or work.

Notification Switch
Would you like to follow the 'College physics: physics of california' conversation and receive update notifications?