| << Chapter < Page | Chapter >> Page > |
Doing an example will make computational savings more obvious.Let's look at the details of a length-8 DFT. As shown on [link] , we first decompose the DFT into two length-4 DFTs, with the outputs added and subtractedtogether in pairs. Considering [link] as the frequency index goes from 0 through 7, we recycle values from the length-4 DFTs into the final calculationbecause of the periodicity of the DFT output. Examining how pairs of outputs are collected together, we create the basiccomputational element known as a butterfly ( [link] ).
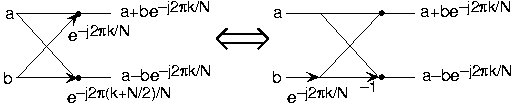
By considering together the computations involving common output frequencies from the two half-length DFTs, we see that the twocomplex multiplies are related to each other, and we can reduce our computational work even further. By further decomposing thelength-4 DFTs into two length-2 DFTs and combining their outputs, we arrive at the diagram summarizing the length-8 fastFourier transform ( [link] ). Although most of the complex multiplies are quite simple(multiplying by means negating real and imaginary parts), let's count those for purposes of evaluating the complexity as full complexmultiplies. We have complex multiplies and additions for each stage and stages, making the number of basic computations as predicted.
Note that the ordering of the input sequence in the two parts of [link] aren't quite the same. Why not? How is the ordering determined?
The upper panel has not used the FFT algorithm to compute the length-4 DFTs while the lower one has. The ordering isdetermined by the algorithm.
We now have a way of computing the spectrum for an arbitrary signal: The Discrete Fourier Transform (DFT) computes the spectrum at equally spaced frequencies from a length- sequence. An issue that never arises in analog "computation," like that performed by a circuit, ishow much work it takes to perform the signal processing operation such as filtering. In computation, this considerationtranslates to the number of basic computational steps required to perform the needed processing. The number of steps, known asthe complexity , becomes equivalent to how long the computation takes (how long must we wait for ananswer). Complexity is not so much tied to specific computers or programming languages but to how many steps are required on anycomputer. Thus, a procedure's stated complexity says that the time taken will be proportional to some function of the amount of data used in the computation and theamount demanded.
For example, consider the formula for the discrete Fourier transform. For each frequency we chose, we must multiply eachsignal value by a complex number and add together the results. For a real-valued signal, each real-times-complexmultiplication requires two real multiplications, meaning we have multiplications to perform. To add the results together, we must keep the real and imaginary partsseparate. Adding numbers requires additions. Consequently, each frequency requires basic computational steps. As we have frequencies, the total number of computations is .
In complexity calculations, we only worry about what happens as the data lengths increase, and take the dominantterm—here the term—as reflecting how much work is involved in making the computation. As multiplicative constants don'tmatter since we are making a "proportional to" evaluation, we find the DFT is an computational procedure. This notation is read "order -squared". Thus, if we double the length of the data, we would expect that thecomputation time to approximately quadruple.
In making the complexity evaluation for the DFT, we assumed the data to be real. Three questionsemerge. First of all, the spectra of such signals have conjugate symmetry, meaning that negative frequency components( in the DFT ) can be computed from the corresponding positive frequency components. Does thissymmetry change the DFT's complexity?
Secondly, suppose the data are complex-valued; what is the DFT's complexity now?
Finally, a less important but interesting question is suppose we want frequency values instead of ; now what is the complexity?
When the signal is real-valued, we may only need half the spectral values, but the complexity remainsunchanged. If the data are complex-valued, which demands retaining all frequency values, the complexity is again thesame. When only frequencies are needed, the complexity is .
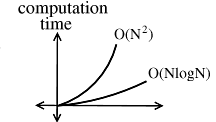
How much better is O(NlogN) than O( )?
| 100 | |||||
Say you have a 1 MFLOP machine (a million "floating point" operations per second). Let .
An O( ) algorithm takes flors → seconds ≃ 11.5 days.
An O( ) algorithm takes Flors → 6 seconds.
3 megapixel digital camera spits out numbers for each picture. So for two point sequences and . If computing directly: O( ) operations.
taking FFTs -- O(NlogN)
multiplying FFTs -- O(N)
inverse FFTs -- O(NlogN).
the total complexity is O(NlogN).
Other "fast" algorithms have been discovered, most of which make use of how many common factors the transform length N has. Innumber theory, the number of prime factors a given integer has measures how composite it is. The numbers 16 and 81 are highly composite (equaling and respectively), the number 18 is less so ( ), and 17 not at all (it's prime). In over thirty years of Fourier transform algorithm development, the originalCooley-Tukey algorithm is far and away the most frequently used. It is so computationally efficient that power-of-twotransform lengths are frequently used regardless of what the actual length of the data. It is even well established that the FFT, alongside the digital computer, were almost completely responsible forthe "explosion" of DSP in the 60's.

Notification Switch
Would you like to follow the 'Signals and systems' conversation and receive update notifications?