12.4 The regression equation  (Page 4/2)

Data rarely fit a straight line exactly. Usually, you must be satisfied with rough predictions. Typically, you have a set of data whose scatter plot appears to "fit" a straight line. This is called a Line of Best Fit or Least Squares Line .

Optional collaborative classroom activity

If you know a person's pinky (smallest) finger length, do you think you could predict that person's height? Collect data from your class (pinky finger length, in inches). Theindependent variable, $x$ , is pinky finger length and the dependent variable, $y$ , is height.

For each set of data, plot the points on graph paper. Make your graph big enough and use a ruler . Then "by eye" draw a line that appears to "fit" the data. For your line, pick two convenient points and use them to find the slope of the line. Find the y-intercept ofthe line by extending your lines so they cross the y-axis. Using the slopes and the y-intercepts, write your equation of "best fit". Do you think everyone will have the sameequation? Why or why not?

Using your equation, what is the predicted height for a pinky length of 2.5 inches?

A random sample of 11 statistics students produced the following data where $x$ is the third exam score, out of 80, and $y$ is the final exam score, out of 200. Can you predict the final exam score of a random student if you know the third exam score?

x (third exam score)	y (final exam score)
65	175
67	133
71	185
71	163
66	126
75	198
67	153
70	163
71	159
69	151
69	159

Got questions? Get instant answers now!

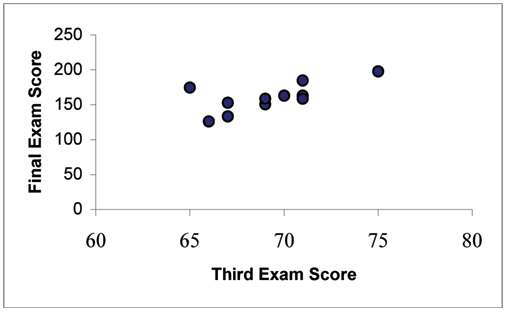
The third exam score, $x$ , is the independent variable and the final exam score, $y$ , is the dependent variable. We will plot a regression line that best "fits" the data. If each of youwere to fit a line "by eye", you would draw different lines. We can use what is called a least-squares regression line to obtain the best fit line.

Consider the following diagram. Each point of data is of the the form $(x,y)$ and each point of the line of best fit using least-squares linear regression has the form $(x,\hat{y})$ .

The $\hat{y}$ is read "y hat" and is the estimated value of $y$ . It is the value of $y$ obtained using the regression line. It is not generally equal to $y$ from data.

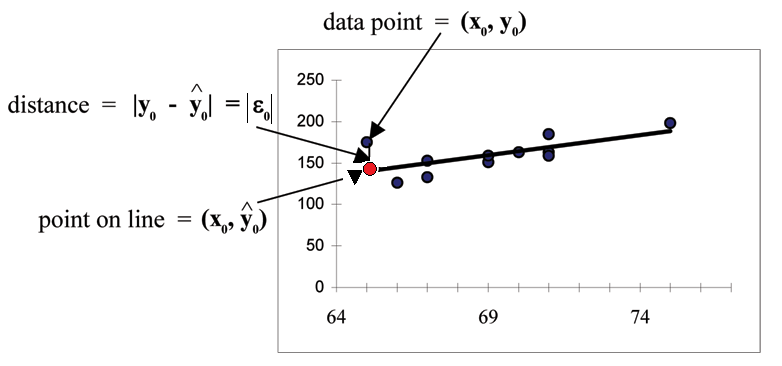
The term $y_0-{\hat{y}}_0={\epsilon }_0$ is called the "error" or residual . It is not an error in the sense of a mistake. The absolute value of a residual measures the vertical distance between the actual value of $y$ and the estimated value of $y$ . In other words, it measures the vertical distance between the actual data point and the predicted point on the line.

If the observed data point lies above the line, the residual is positive, and the line underestimates the actual data value for $y$ . If the observed data point lies below the line, the residual is negative, and the line overestimates that actual data value for $y$ .

In the diagram above, $y_0-{\hat{y}}_0={\epsilon }_0$ is the residual for the point shown. Here the point lies above the line and the residual is positive.