12.4 Test of independence  (Page 2/3)

The observed table and the question at the end of the problem, "Are the number of hours volunteered independent of the type of volunteer?" tell you this is a test ofindependence. The two factors are number of hours volunteered and type of volunteer . This test is always right-tailed.

$H_o$ : The number of hours volunteered is independent of the type of volunteer.

$H_a$ : The number of hours volunteered is dependent on the type of volunteer.

The expected table is:

For example, the calculation for the expected frequency for the top left cell is

$E=\frac{\text{(row total)(column total)}}{\text{total number surveyed}}=\frac{255\cdot 298}{839}=90.57$

Calculate the test statistic: ${\chi }^2=12.99$ (calculator or computer)

Distribution for the test: ${\chi }_4^2$

$\text{df}=(\text{3 columns}-1)(\text{3 rows}-1)=\left(2\right)\left(2\right)=4$

Graph:

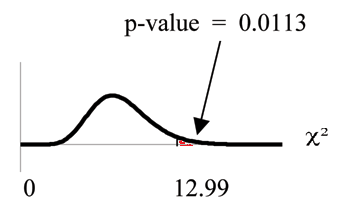
Probability statement: $\text{p-value}=P({\chi }^2>12.99)=0.0113$

Compare $\alpha$ and the $\text{p-value}$ : Since no $\alpha$ is given, assume $\alpha =0.05$ . $\text{p-value}=0.0113$ . $\alpha >\text{p-value}$ .

Make a decision: Since $\alpha >\text{p-value}$ , reject $H_o$ . This means that the factors are not independent.

Conclusion: At a 5% level of significance, from the data, there is sufficient evidence to conclude that the number of hours volunteered and the type of volunteer aredependent on one another.

For the above example, if there had been another type of volunteer, teenagers, whatwould the degrees of freedom be?

TI-83+ and TI-84 calculator: Press the MATRX key and arrow over to EDIT . Press 1:[A] . Press 3 ENTER 3 ENTER . Enter the table values by row from Example 11-6. Press ENTER after each. Press 2nd QUIT . Press STAT and arrow over to TESTS . Arrow down to C:χ2-TEST . Press ENTER . You should see Observed:[A] and Expected:[B] . Arrow down to Calculate . Press ENTER . The test statistic is 12.9909 and the $\text{p-value}=0.0113$ . Do the procedure a second time but arrow down to Draw instead of calculate .