12.2 The first law of thermodynamics and some simple processes

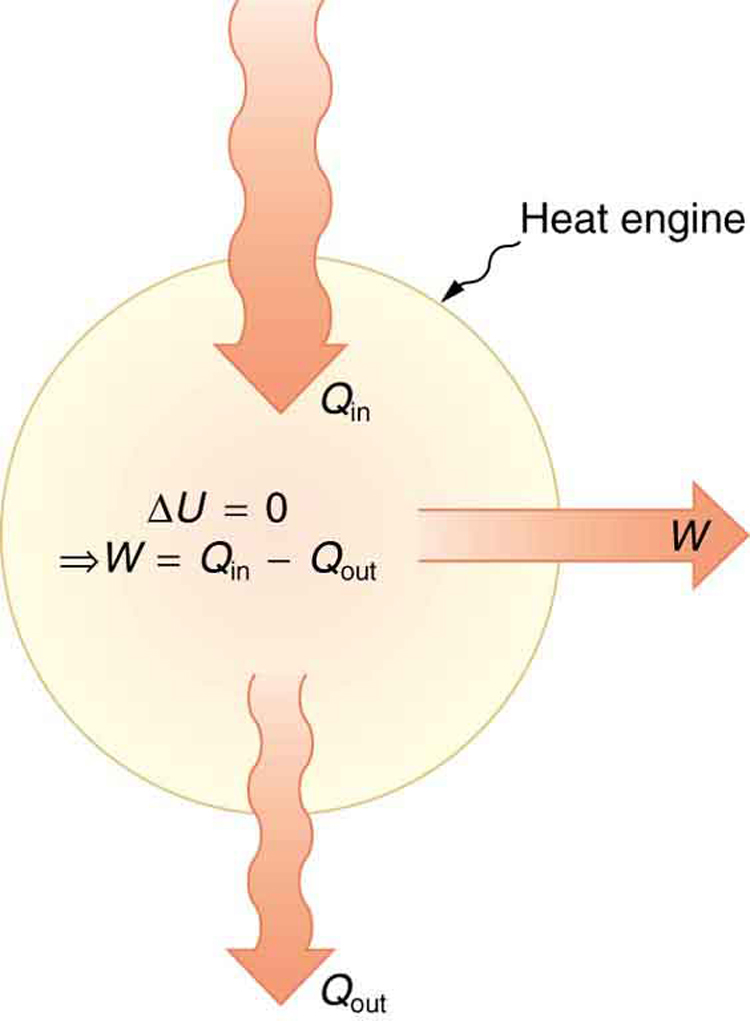
One of the most important things we can do with heat transfer is to use it to do work for us. Such a device is called a heat engine    . Car engines and steam turbines that generate electricity are examples of heat engines. [link] shows schematically how the first law of thermodynamics applies to the typical heat engine.

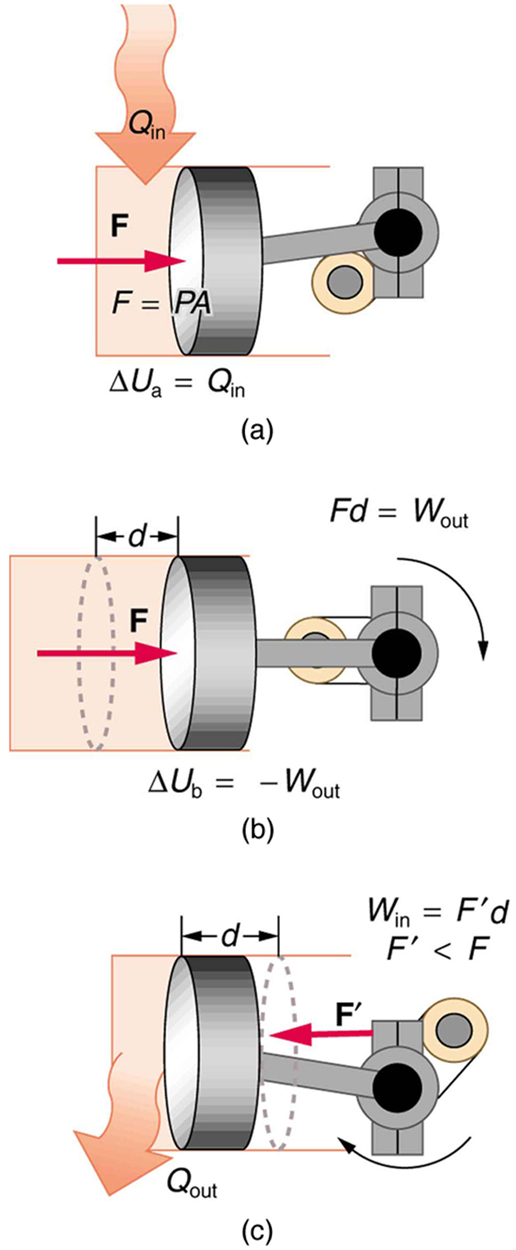
The illustrations above show one of the ways in which heat transfer does work. Fuel combustion produces heat transfer to a gas in a cylinder, increasing the pressure of the gas and thereby the force it exerts on a movable piston. The gas does work on the outside world, as this force moves the piston through some distance. Heat transfer to the gas cylinder results in work being done. To repeat this process, the piston needs to be returned to its starting point. Heat transfer now occurs from the gas to the surroundings so that its pressure decreases, and a force is exerted by the surroundings to push the piston back through some distance. Variations of this process are employed daily in hundreds of millions of heat engines. We will examine heat engines in detail in the next section. In this section, we consider some of the simpler underlying processes on which heat engines are based.

PV Diagrams and their relationship to work done on or by a gas

A process by which a gas does work on a piston at constant pressure is called an isobaric process    . Since the pressure is constant, the force exerted is constant and the work done is given as

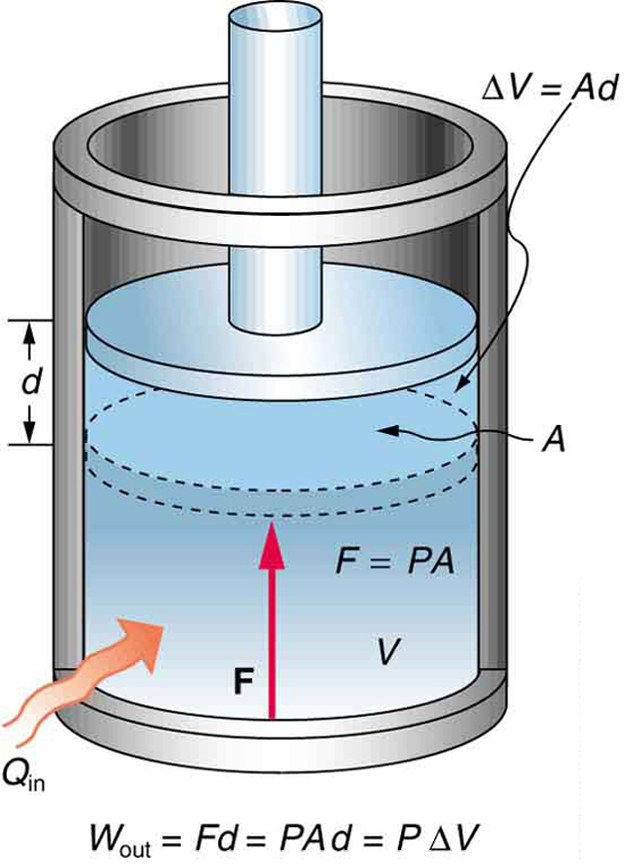
See the symbols as shown in [link] . Now $F=\text{PA}$ , and so

Because the volume of a cylinder is its cross-sectional area $A$ times its length $d$ , we see that $\text{Ad}=\mathrm{\Delta }V$ , the change in volume; thus,