| << Chapter < Page | Chapter >> Page > |
Fill a bathtub half-full of water. Take a toy boat or some other object that floats in water. Unplug the drain so water starts to drain. Try pushing the boat from one side of the tub to the other and perpendicular to the flow of water. Which way do you need to push the boat so that it ends up immediately opposite? Compare the directions of the flow of water, heading of the boat, and actual velocity of the boat.
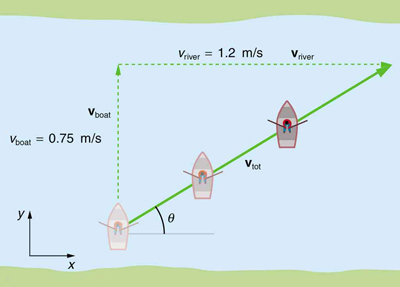
Refer to [link] , which shows a boat trying to go straight across the river. Let us calculate the magnitude and direction of the boat’s velocity relative to an observer on the shore, . The velocity of the boat, , is 0.75 m/s in the -direction relative to the river and the velocity of the river, , is 1.20 m/s to the right.
Strategy
We start by choosing a coordinate system with its -axis parallel to the velocity of the river, as shown in [link] . Because the boat is directed straight toward the other shore, its velocity relative to the water is parallel to the -axis and perpendicular to the velocity of the river. Thus, we can add the two velocities by using the equations and directly.
Solution
The magnitude of the total velocity is
where
and
Thus,
yielding
The direction of the total velocity is given by:
This equation gives
Discussion
Both the magnitude and the direction of the total velocity are consistent with [link] . Note that because the velocity of the river is large compared with the velocity of the boat, it is swept rapidly downstream. This result is evidenced by the small angle (only ) the total velocity has relative to the riverbank.
Calculate the wind velocity for the situation shown in [link] . The plane is known to be moving at 45.0 m/s due north relative to the air mass, while its velocity relative to the ground (its total velocity) is 38.0 m/s in a direction west of north.
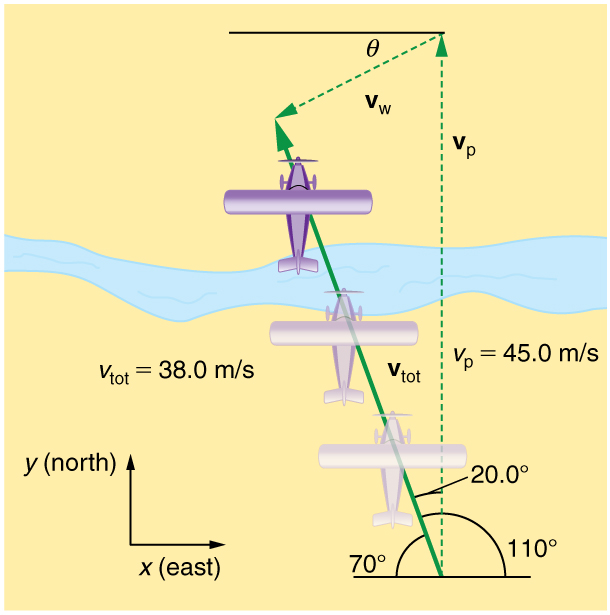
Strategy
In this problem, somewhat different from the previous example, we know the total velocity and that it is the sum of two other velocities, (the wind) and (the plane relative to the air mass). The quantity is known, and we are asked to find . None of the velocities are perpendicular, but it is possible to find their components along a common set of perpendicular axes. If we can find the components of , then we can combine them to solve for its magnitude and direction. As shown in [link] , we choose a coordinate system with its x -axis due east and its y -axis due north (parallel to ). (You may wish to look back at the discussion of the addition of vectors using perpendicular components in Vector Addition and Subtraction: Analytical Methods .)

Notification Switch
Would you like to follow the 'Physics 110 at une' conversation and receive update notifications?