11.8 Binding energy  (Page 2/5)

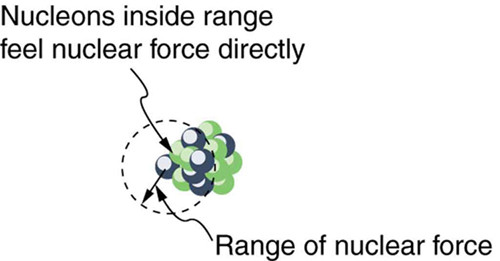
What patterns and insights are gained from an examination of the binding energy of various nuclides? First, we find that BE is approximately proportional to the number of nucleons $A$ in any nucleus. About twice as much energy is needed to pull apart a nucleus like ${}^{\text{24}}\text{Mg}$ compared with pulling apart ${}^{\text{12}}\text{C}$ , for example. To help us look at other effects, we divide BE by $A$ and consider the binding energy per nucleon    , $\text{BE}/A$ . The graph of $\text{BE}/A$ in [link] reveals some very interesting aspects of nuclei. We see that the binding energy per nucleon averages about 8 MeV, but is lower for both the lightest and heaviest nuclei. This overall trend, in which nuclei with $A$ equal to about 60 have the greatest $\text{BE}/A$ and are thus the most tightly bound, is due to the combined characteristics of the attractive nuclear forces and the repulsive Coulomb force. It is especially important to note two things—the strong nuclear force is about 100 times stronger than the Coulomb force, and the nuclear forces are shorter in range compared to the Coulomb force. So, for low-mass nuclei, the nuclear attraction dominates and each added nucleon forms bonds with all others, causing progressively heavier nuclei to have progressively greater values of $\text{BE}/A$ . This continues up to $A\approx \text{60}$ , roughly corresponding to the mass number of iron. Beyond that, new nucleons added to a nucleus will be too far from some others to feel their nuclear attraction. Added protons, however, feel the repulsion of all other protons, since the Coulomb force is longer in range. Coulomb repulsion grows for progressively heavier nuclei, but nuclear attraction remains about the same, and so $\text{BE}/A$ becomes smaller. This is why stable nuclei heavier than $A\approx \text{40}$ have more neutrons than protons. Coulomb repulsion is reduced by having more neutrons to keep the protons farther apart (see [link] ).

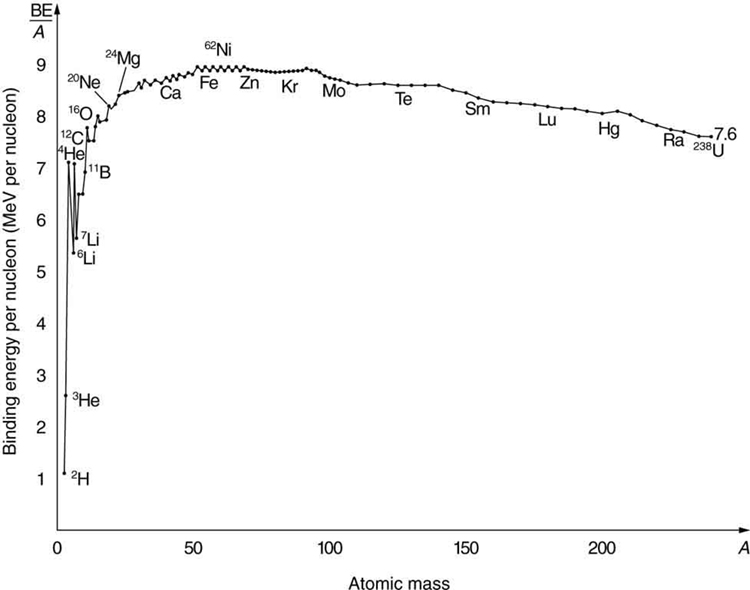
There are some noticeable spikes on the $\text{BE}/A$ graph, which represent particularly tightly bound nuclei. These spikes reveal further details of nuclear forces, such as confirming that closed-shell nuclei (those with magic numbers of protons or neutrons or both) are more tightly bound. The spikes also indicate that some nuclei with even numbers for $Z$ and $N$ , and with $Z=N$ , are exceptionally tightly bound. This finding can be correlated with some of the cosmic abundances of the elements. The most common elements in the universe, as determined by observations of atomic spectra from outer space, are hydrogen, followed by ${}^4\text{He}$ , with much smaller amounts of ${}^{\text{12}}\text{C}$ and other elements. It should be noted that the heavier elements are created in supernova explosions, while the lighter ones are produced by nuclear fusion during the normal life cycles of stars, as will be discussed in subsequent chapters. The most common elements have the most tightly bound nuclei. It is also no accident that one of the most tightly bound light nuclei is ${}^4\text{He}$ , emitted in $\alpha$ decay.