11.7 Test of a single variance

Even though we are given the population standard deviation, we can set the test up using the population variance as follows.

• $H_o$ : ${\sigma }^2=5^2$
• $H_a$ : ${\sigma }^2>5^2$

Since the claim is that a single line causes lower variation, this is a test of a single variance. The parameter is the population variance, ${\sigma }^2$ , or the population standard deviation, $\sigma$ .

Random Variable: The sample standard deviation, $s$ , is the random variable. Let $s$ = standard deviation for the waiting times.

• $H_o$ : ${\sigma }^2={7.2}^2$
• $H_a$ : ${\sigma }^2$ $$ ${7.2}^2$

The word "lower" tells you this is a left-tailed test.

Distribution for the test: ${\chi }_{24}^2$ , where:

• $n$ = the number of customers sampled
• $\text{df}=n-1=25-1=24$

Calculate the test statistic:

${\chi }^2=\frac{(n-1)\cdot s^2}{{\sigma }^2}=\frac{(25-1)\cdot {3.5}^2}{{7.2}^2}=5.67$

where $n=25$ , $s=3.5$ , and $\sigma =7.2$ .

Graph:

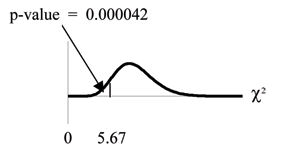
Probability statement: $\text{p-value}=P({\chi }^2<5.67)=0.000042$

Compare $\alpha$ and the p-value: $\alpha =0.05\text{p-value}=0.000042\alpha >\text{p-value}$

Make a decision: Since $\alpha >\text{p-value}$ , reject $H_o$ .

This means that you reject ${\sigma }^2={7.2}^2$ . In other words, you do not think the variation in waiting times is 7.2 minutes, but lower.

Conclusion: At a 5% level of significance, from the data, there is sufficient evidence to conclude that a single line causes a lower variation among the waiting times or with a single line, the customer waiting times vary less than 7.2 minutes.

TI-83+ and TI-84 calculators : In 2nd DISTR , use 7:χ2cdf . The syntax is (lower, upper, df) for the parameter list. For Example 11-9, χ2cdf(-1E99,5.67,24) . The $\text{p-value}=0.000042$ .