11.6 Temperature change and heat capacity  (Page 23/6)

One of the major effects of heat transfer is temperature change: heating increases the temperature while cooling decreases it. We assume that there is no phase change and that no work is done on or by the system. Experiments show that the transferred heat depends on three factors—the change in temperature, the mass of the system, and the substance and phase of the substance.

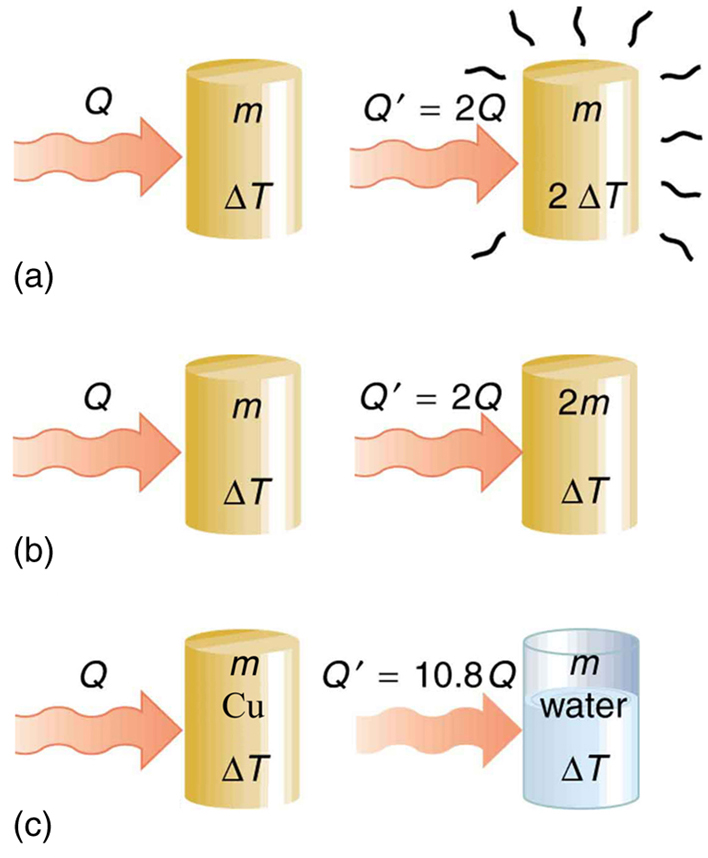
The dependence on temperature change and mass are easily understood. Owing to the fact that the (average) kinetic energy of an atom or molecule is proportional to the absolute temperature, the internal energy of a system is proportional to the absolute temperature and the number of atoms or molecules. Owing to the fact that the transferred heat is equal to the change in the internal energy, the heat is proportional to the mass of the substance and the temperature change. The transferred heat also depends on the substance so that, for example, the heat necessary to raise the temperature is less for alcohol than for water. For the same substance, the transferred heat also depends on the phase (gas, liquid, or solid).

Values of specific heat must generally be looked up in tables, because there is no simple way to calculate them. In general, the specific heat also depends on the temperature. [link] lists representative values of specific heat for various substances. Except for gases, the temperature and volume dependence of the specific heat of most substances is weak. We see from this table that the specific heat of water is five times that of glass and ten times that of iron, which means that it takes five times as much heat to raise the temperature of water the same amount as for glass and ten times as much heat to raise the temperature of water as for iron. In fact, water has one of the largest specific heats of any material, which is important for sustaining life on Earth.