11.5 Simple machines

Simple machines are devices that can be used to multiply or augment a force that we apply – often at the expense of a distance through which we apply the force. The word for “machine” comes from the Greek word meaning “to help make things easier.” Levers, gears, pulleys, wedges, and screws are some examples of machines. Energy is still conserved for these devices because a machine cannot do more work than the energy put into it. However, machines can reduce the input force that is needed to perform the job. The ratio of output to input force magnitudes for any simple machine is called its mechanical advantage    (MA).

One of the simplest machines is the lever, which is a rigid bar pivoted at a fixed place called the fulcrum. Torques are involved in levers, since there is rotation about a pivot point. Distances from the physical pivot of the lever are crucial, and we can obtain a useful expression for the MA in terms of these distances.

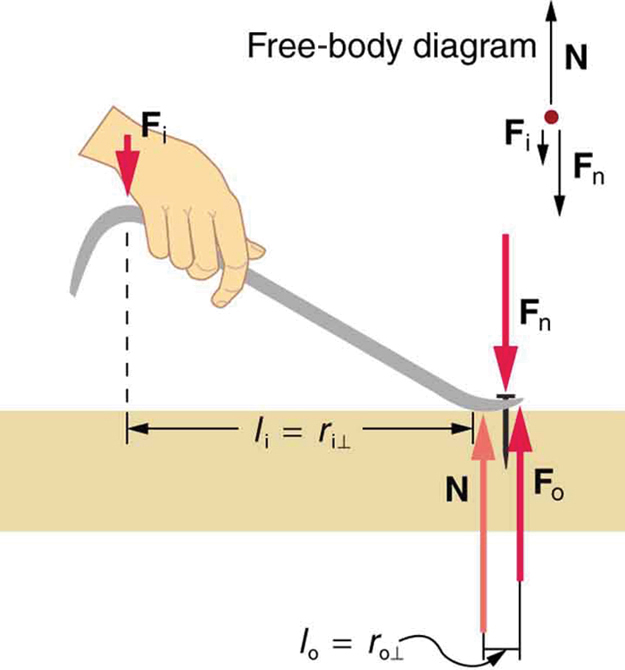
[link] shows a lever type that is used as a nail puller. Crowbars, seesaws, and other such levers are all analogous to this one. ${\mathbf{\text{F}}}_{\text{i}}$ is the input force and ${\mathbf{\text{F}}}_{\text{o}}$ is the output force. There are three vertical forces acting on the nail puller (the system of interest) – these are ${\mathbf{\text{F}}}_{\text{i}},{\mathbf{\text{F}}}_{\text{o}},$ and $\mathbf{\text{N}}$ . ${\mathbf{\text{F}}}_{\text{n}}$ is the reaction force back on the system, equal and opposite to ${\mathbf{\text{F}}}_{\text{o}}$ . (Note that ${\mathbf{\text{F}}}_{\text{o}}$ is not a force on the system.) $\mathbf{\text{N}}$ is the normal force upon the lever, and its torque is zero since it is exerted at the pivot. The torques due to ${\mathbf{\text{F}}}_{\text{i}}$ and ${\mathbf{\text{F}}}_{\text{n}}$ must be equal to each other if the nail is not moving, to satisfy the second condition for equilibrium $\left(\text{net}\tau =0\right)$ . (In order for the nail to actually move, the torque due to ${\mathbf{\text{F}}}_{\text{i}}$ must be ever-so-slightly greater than torque due to ${\mathbf{\text{F}}}_{\text{n}}$ .) Hence,

where $l_{\text{i}}$ and $l_{\text{o}}$ are the distances from where the input and output forces are applied to the pivot, as shown in the figure. Rearranging the last equation gives

What interests us most here is that the magnitude of the force exerted by the nail puller, $F_{\text{o}}$ , is much greater than the magnitude of the input force applied to the puller at the other end, $F_{\text{i}}$ . For the nail puller,

This equation is true for levers in general. For the nail puller, the MA is certainly greater than one. The longer the handle on the nail puller, the greater the force you can exert with it.

Two other types of levers that differ slightly from the nail puller are a wheelbarrow and a shovel, shown in [link] . All these lever types are similar in that only three forces are involved – the input force, the output force, and the force on the pivot – and thus their MAs are given by $\text{MA}=\frac{F_{\text{o}}}{F_{\text{i}}}$ and $\text{MA}=\frac{d_1}{d_2}$ , with distances being measured relative to the physical pivot. The wheelbarrow and shovel differ from the nail puller because both the input and output forces are on the same side of the pivot.