11.3 Simple harmonic motion: a special periodic motion  (Page 3/7)

where $v_{\text{max}}=\mathrm{2\pi }X/T=X\sqrt{k/m}$ . The object has zero velocity at maximum displacement—for example, $v=0$ when $t=0$ , and at that time $x=X$ . The minus sign in the first equation for $v(t)$ gives the correct direction for the velocity. Just after the start of the motion, for instance, the velocity is negative because the system is moving back toward the equilibrium point. Finally, we can get an expression for acceleration using Newton’s second law. [Then we have $x(t),v(t),t,$ and $a(t)$ , the quantities needed for kinematics and a description of simple harmonic motion.] According to Newton’s second law, the acceleration is $a=F/m=\text{kx}/m$ . So, $a(t)$ is also a cosine function:

Hence, $a(t)$ is directly proportional to and in the opposite direction to $x(t)$ .

[link] shows the simple harmonic motion of an object on a spring and presents graphs of $x(t),v(t),$ and $a(t)$ versus time.

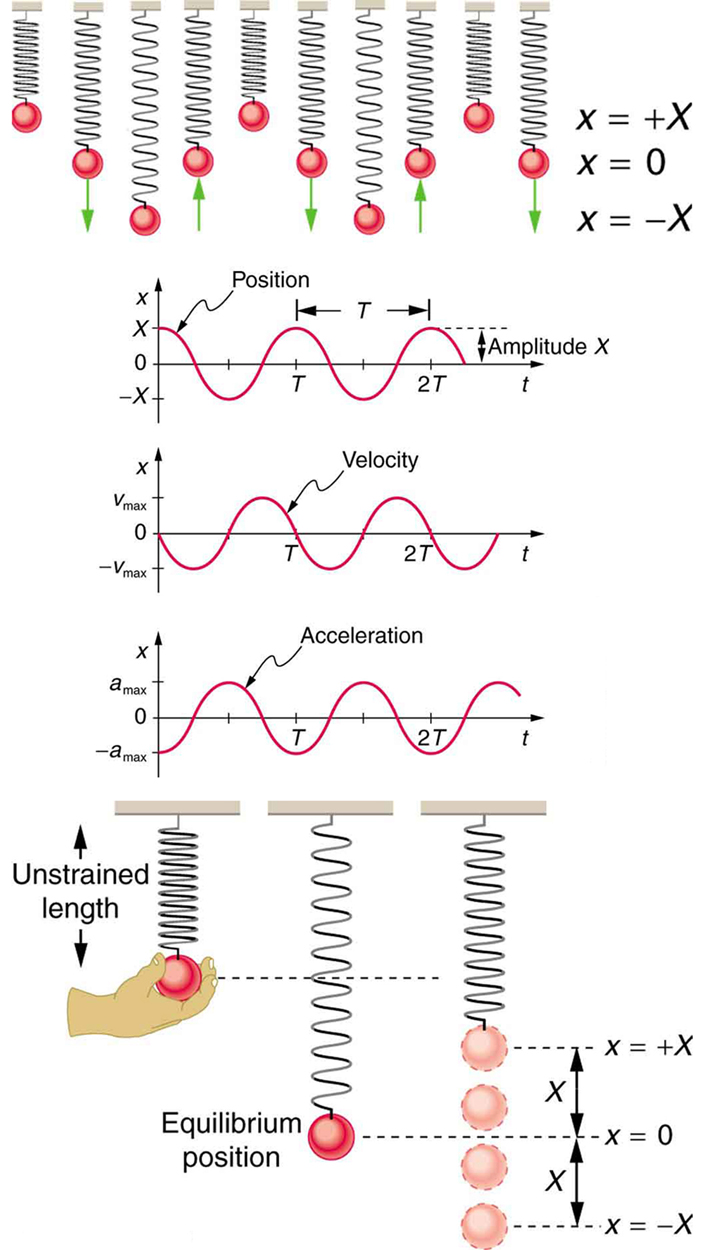
The most important point here is that these equations are mathematically straightforward and are valid for all simple harmonic motion. They are very useful in visualizing waves associated with simple harmonic motion, including visualizing how waves add with one another.

Phet explorations: masses and springs

A realistic mass and spring laboratory. Hang masses from springs and adjust the spring stiffness and damping. You can even slow time. Transport the lab to different planets. A chart shows the kinetic, potential, and thermal energy for each spring.

Section summary

• Simple harmonic motion is oscillatory motion for a system that can be described only by Hooke’s law. Such a system is also called a simple harmonic oscillator.
• Maximum displacement is the amplitude $X$ . The period $T$ and frequency $f$ of a simple harmonic oscillator are given by

  $T=\mathrm{2\pi }\sqrt{\frac{m}{k}}$ and $f=\frac{1}{\mathrm{2\pi }}\sqrt{\frac{k}{m}}$ , where $m$ is the mass of the system.

• Displacement in simple harmonic motion as a function of time is given by $x(t)=X\text{cos}\frac{\mathrm{2\pi }t}{T}.$
• The velocity is given by $v(t)=-v_{\text{max}}\text{sin}\frac{\mathrm{2\pi }\text{t}}{T}$ , where $v_{\text{max}}=\sqrt{k/m}X$ .
• The acceleration is found to be $a(t)=-\frac{\mathrm{kX}}{m}\text{cos}\frac{\mathrm{2\pi }t}{T}.$