1. Home
  2. Ut austin - principles of
  3. Nuclear
  4. Radioactive decay

11.3 Radioactive decay  (Page 4/21)

<< Chapter < Page
  Ut austin - principles of     Page 4 / 21
Chapter >> Page >
A graph is shown where the x-axis is labeled “Number of neutrons, open parenthesis, n, close parenthesis” and has values of 122 to 148 in increments of 2. The y-axis is labeled “Atomic number” and has values of 80 to 92 in increments of 1. Two types of arrows are used in this graph to connect the points. Green arrows are labeled as “alpha decay” while red arrows are labeled “beta decay.” Beginning at the point “92, 146” that is labeled “superscript 238, U,” a green arrow connects this point to the second point “90, 144” which is labeled “superscript 234, T h.” A red arrow connect this to the third point “91, 143” which is labeled “superscript 234, P a” which is connected to the fourth point “92, 142” by a red arrow and which is labeled “superscript 234, U.” A green arrow leads to the next point, “90, 140” which is labeled “superscript 230, T h” and is connected by a green arrow to the sixth point, “88, 138” which is labeled “superscript 226, R a” that is in turn connected by a green arrow to the seventh point “86, 136” which is labeled “superscript 222, Ra.” The eighth point, at “84, 134” is labeled “superscript 218, P o” and has green arrows leading to it and away from it to the ninth point “82, 132” which is labeled “superscript 214, Pb” which is connected by a red arrow to the tenth point, “83, 131” which is labeled “superscript 214, B i.” A red arrow leads to the eleventh point “84, 130” which is labeled “superscript 214, P o” and a green arrow leads to the twelvth point “82, 128” which is labeled “superscript 210, P b.” A red arrow leads to the thirteenth point “83, 127” which is labeled “superscript 210, B i” and a red arrow leads to the fourteenth point “84, 126” which is labeled “superscript 210, P o.” The final point is labeled “82, 124” and “superscript 206, P b.”
Uranium-238 undergoes a radioactive decay series consisting of 14 separate steps before producing stable lead-206. This series consists of eight α decays and six β decays.

Radioactive half-lives

Radioactive decay follows first-order kinetics. Since first-order reactions have already been covered in detail in the kinetics chapter, we will now apply those concepts to nuclear decay reactions. Each radioactive nuclide has a characteristic, constant half-life ( t 1/2 ), the time required for half of the atoms in a sample to decay. An isotope’s half-life allows us to determine how long a sample of a useful isotope will be available, and how long a sample of an undesirable or dangerous isotope must be stored before it decays to a low-enough radiation level that is no longer a problem.

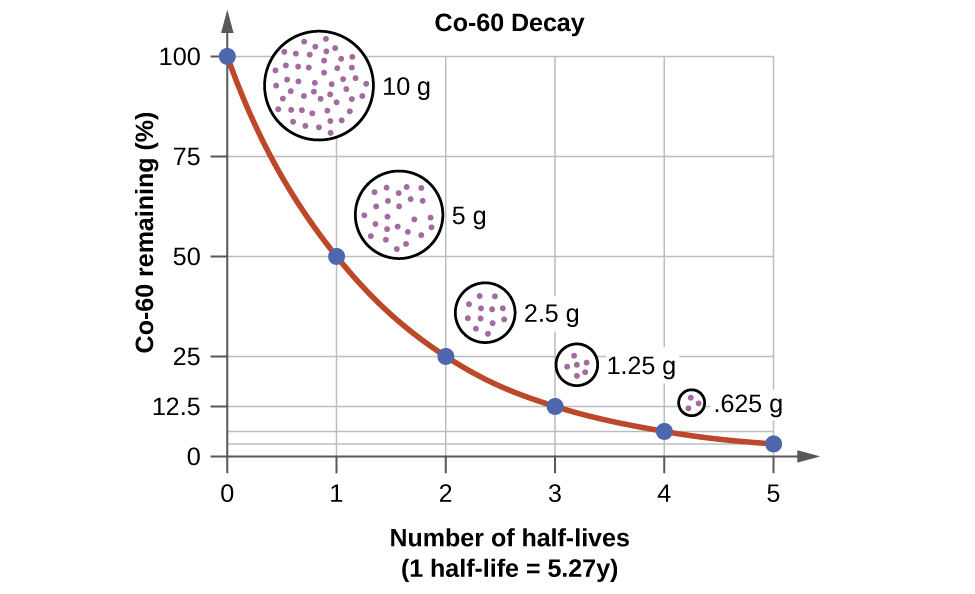
For example, cobalt-60, an isotope that emits gamma rays used to treat cancer, has a half-life of 5.27 years ( [link] ). In a given cobalt-60 source, since half of the 27 60 Co nuclei decay every 5.27 years, both the amount of material and the intensity of the radiation emitted is cut in half every 5.27 years. (Note that for a given substance, the intensity of radiation that it produces is directly proportional to the rate of decay of the substance and the amount of the substance.) This is as expected for a process following first-order kinetics. Thus, a cobalt-60 source that is used for cancer treatment must be replaced regularly to continue to be effective.

A graph, titled “C o dash 60 Decay,” is shown where the x-axis is labeled “C o dash 60 remaining, open parenthesis, percent sign, close parenthesis” and has values of 0 to 100 in increments of 25. The y-axis is labeled “Number of half dash lives” and has values of 0 to 5 in increments of 1. The first point, at “0, 100” has a circle filled with tiny dots drawn near it labeled “10 g.” The second point, at “1, 50” has a smaller circle filled with tiny dots drawn near it labeled “5 g.” The third point, at “2, 25” has a small circle filled with tiny dots drawn near it labeled “2.5 g.” The fourth point, at “3, 12.5” has a very small circle filled with tiny dots drawn near it labeled “1.25 g.” The last point, at “4, 6.35” has a tiny circle filled with tiny dots drawn near it labeled.”625 g.”
For cobalt-60, which has a half-life of 5.27 years, 50% remains after 5.27 years (one half-life), 25% remains after 10.54 years (two half-lives), 12.5% remains after 15.81 years (three half-lives), and so on.

Since nuclear decay follows first-order kinetics, we can adapt the mathematical relationships used for first-order chemical reactions. We generally substitute the number of nuclei, N , for the concentration. If the rate is stated in nuclear decays per second, we refer to it as the activity of the radioactive sample. The rate for radioactive decay is:

decay rate = λN with λ = the decay constant for the particular radioisotope

The decay constant, λ , which is the same as a rate constant discussed in the kinetics chapter. It is possible to express the decay constant in terms of the half-life, t 1/2 :

λ = ln 2 t 1 / 2 = 0.693 t 1 / 2 or t 1 / 2 = ln 2 λ = 0.693 λ

The first-order equations relating amount, N , and time are:

N t = N 0 e − k t or t = − 1 λ ln ( N t N 0 )

where N 0 is the initial number of nuclei or moles of the isotope, and N t is the number of nuclei/moles remaining at time t . [link] applies these calculations to find the rates of radioactive decay for specific nuclides.

Rates of radioactive decay

27 60 Co decays with a half-life of 5.27 years to produce 28 60 Ni .

(a) What is the decay constant for the radioactive disintegration of cobalt-60?

(b) Calculate the fraction of a sample of the 27 60 Co isotope that will remain after 15 years.

(c) How long does it take for a sample of 27 60 Co to disintegrate to the extent that only 2.0% of the original amount remains?

Solution

(a) The value of the rate constant is given by:

λ = ln 2 t 1 / 2 = 0.693 5.27 y = 0.132 y −1

(b) The fraction of 27 60 Co that is left after time t is given by N t N 0 . Rearranging the first-order relationship N t = N 0 e – λt to solve for this ratio yields:

N t N 0 = e − λ t = e − ( 0.132 /y ) ( 15.0 /y ) = 0.138

The fraction of 27 60 Co that will remain after 15.0 years is 0.138. Or put another way, 13.8% of the 27 60 Co originally present will remain after 15 years.

(c) 2.00% of the original amount of 27 60 Co is equal to 0.0200 × N 0 . Substituting this into the equation for time for first-order kinetics, we have:

t = − 1 λ ln ( N t N 0 ) = − 1 0.132 y −1 ln ( 0.0200 × N 0 N 0 ) = 29.6 y

Check your learning

Radon-222, 86 222 Rn , has a half-life of 3.823 days. How long will it take a sample of radon-222 with a mass of 0.750 g to decay into other elements, leaving only 0.100 g of radon-222?

Answer:

11.1 days

Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>
Practice Key Terms 12

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Ut austin - principles of chemistry. OpenStax CNX. Mar 31, 2016 Download for free at http://legacy.cnx.org/content/col11830/1.13
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Ut austin - principles of chemistry' conversation and receive update notifications?

Ask