11.3 Goodness-of-fit test  (Page 3/3)

This problem asks you to test whether the far western United States families distribution fits the distribution of the American families. This test is always right-tailed.

The first table contains expected percentages. To get expected ( $E$ ) frequencies, multiply the percentage by 600. The expected frequencies are:

Therefore, the expected frequencies are 60, 96, 330, 66, and 48. In the TI calculators, you can let the calculator do the math. For example, instead of 60,enter .10*600.

$H_o$ : The "number of televisions" distribution of far western United States families is the same as the "number of televisions" distribution of the American population.

$H_a$ : The "number of televisions" distribution of far western United States families is different from the "number of televisions" distribution of the American population.

Distribution for the test: ${\chi }_4^2$ where $\mathrm{df}=\text{(the number of cells)}-1=5-1=4$ .

Calculate the test statistic: ${\chi }^2=29.65$

Graph:

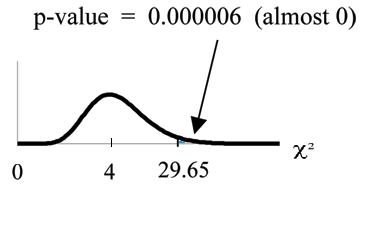
Probability statement: $\text{p-value}=P({\chi }^2>29.65)=0.000006$ .

Compare α and the p-value:

• $\alpha =0.01$
• $\text{p-value}=0.000006$

Make a decision: Since $\alpha >\text{p-value}$ , reject $H_o$ .

This means you reject the belief that the distribution for the far western states is the same as that of the American population as a whole.

Conclusion: At the 1% significance level, from the data, there is sufficient evidence to conclude that the "number of televisions" distribution for the far western United Statesis different from the "number of televisions" distribution for the American population as a whole.

This problem can be set up as a goodness-of-fit problem. The sample space for flipping two fair coins is {HH, HT, TH, TT}. Out of 100 flips, you would expect 25 HH, 25 HT,25 TH, and 25 TT. This is the expected distribution. The question, "Are the coins fair?" is the same as saying, "Does the distribution of the coins (20 HH, 27 HT, 30 TH, 23 TT)fit the expected distribution?"

Random Variable: Let $X$ = the number of heads in one flip of the two coins. $X$ takes on the value 0, 1, 2. (There are 0, 1, or 2 heads in the flip of 2 coins.) Therefore, the number of cells is 3 . Since $X$ = the number of heads, the observed frequencies are 20 (for 2 heads), 57 (for 1 head), and 23 (for 0 heads or both tails). The expectedfrequencies are 25 (for 2 heads), 50 (for 1 head), and 25 (for 0 heads or both tails). This test is right-tailed.

$H_o$ : The coins are fair.

$H_a$ : The coins are not fair.

Distribution for the test: ${\chi }_2^2$ where $\mathrm{df}=3-1=2$ .

Calculate the test statistic: ${\chi }^2=2.14$

Graph:

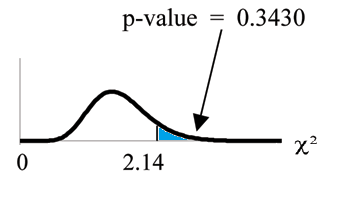
Probability statement: $\text{p-value}=P({\chi }^2>2.14)=0.3430$

Compare $\alpha$ and the p-value:

• $\alpha =0.05$
• $\text{p-value}=0.3430$

Make a decision: Since $\alpha <\text{p-value}$ , do not reject $H_o$ .

Conclusion: There is insufficient evidence to conclude that the coins are not fair.