11.1 Hooke’s law: stress and strain revisited  (Page 3/7)

Calculating stored energy: a tranquilizer gun spring

We can use a toy gun’s spring mechanism to ask and answer two simple questions: (a) How much energy is stored in the spring of a tranquilizer gun that has a force constant of 50.0 N/m and is compressed 0.150 m? (b) If you neglect friction and the mass of the spring, at what speed will a 2.00-g projectile be ejected from the gun?

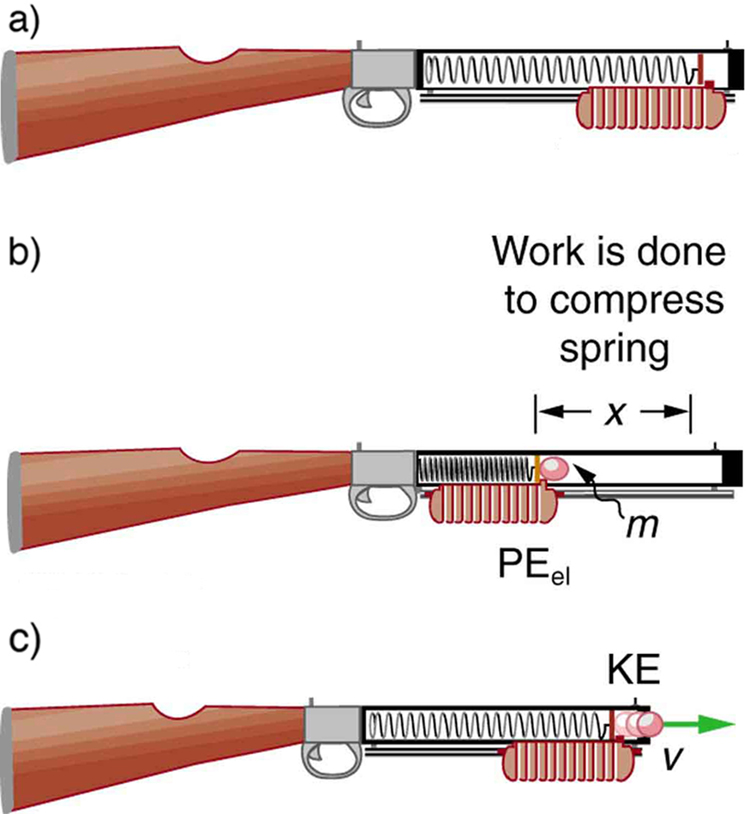
Strategy for a

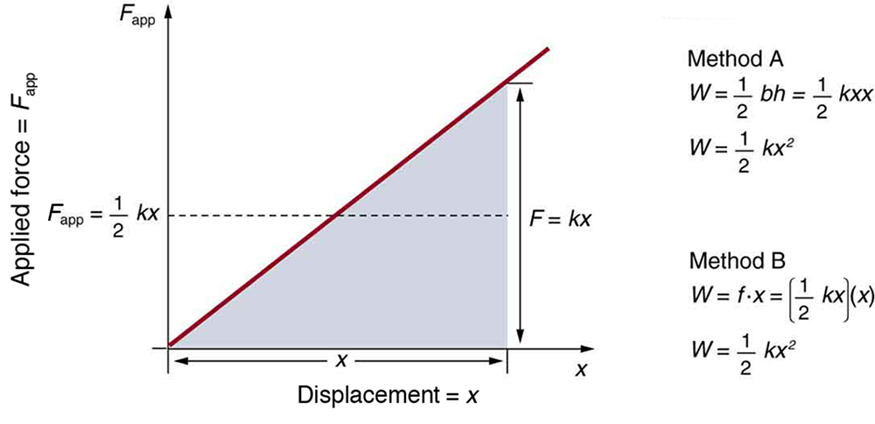
(a): The energy stored in the spring can be found directly from elastic potential energy equation, because $k$ and $x$ are given.

Solution for a

Entering the given values for $k$ and $x$ yields

Strategy for b

Because there is no friction, the potential energy is converted entirely into kinetic energy. The expression for kinetic energy can be solved for the projectile’s speed.

Solution for b

1. Identify known quantities:
   ${\text{KE}}_{\text{f}}={\text{PE}}_{\text{el}}or1/2{\mathit{mv}}^2=(1/2){\mathit{kx}}^2={\text{PE}}_{\mathrm{el}}=0\text{.}\text{563}\text{J}$
2. Solve for $v$ :
   $v={\left[\frac{2{\text{PE}}_{\text{el}}}{m}\right]}^{1/2}={\left[\frac{2\left(0\text{.}\text{563}\text{J}\right)}{0\text{.}\text{002}\text{kg}}\right]}^{1/2}=\text{23}\text{.}7{\left(\text{J/kg}\right)}^{1/2}$
3. Convert units: $23.7\text{m}/\text{s}$

Discussion

(a) and (b): This projectile speed is impressive for a tranquilizer gun (more than 80 km/h). The numbers in this problem seem reasonable. The force needed to compress the spring is small enough for an adult to manage, and the energy imparted to the dart is small enough to limit the damage it might do. Yet, the speed of the dart is great enough for it to travel an acceptable distance.