11.1 Cosmology and particle physics  (Page 9/20)

If a galaxy is 500 Mly away from us, how fast do we expect it to be moving and in what direction?

On average, how far away are galaxies that are moving away from us at 2.0% of the speed of light?

Our solar system orbits the center of the Milky Way galaxy. Assuming a circular orbit 30,000 ly in radius and an orbital speed of 250 km/s, how many years does it take for one revolution? Note that this is approximate, assuming constant speed and circular orbit, but it is representative of the time for our system and local stars to make one revolution around the galaxy.

(a) What is the approximate speed relative to us of a galaxy near the edge of the known universe, some 10 Gly away? (b) What fraction of the speed of light is this? Note that we have observed galaxies moving away from us at greater than $0\text{.}9c$ .

(a) Calculate the approximate age of the universe from the average value of the Hubble constant, $H_0=\text{20}km/s\cdot \text{Mly}$ . To do this, calculate the time it would take to travel 1 Mly at a constant expansion rate of 20 km/s. (b) If deceleration is taken into account, would the actual age of the universe be greater or less than that found here? Explain.

Assuming a circular orbit for the Sun about the center of the Milky Way galaxy, calculate its orbital speed using the following information: The mass of the galaxy is equivalent to a single mass $1\text{.}5\times {\text{10}}^{\text{11}}$ times that of the Sun (or $3\times {\text{10}}^{\text{41}}\text{kg}$ ), located 30,000 ly away.

(a) What is the approximate force of gravity on a 70-kg person due to the Andromeda galaxy, assuming its total mass is ${\text{10}}^{\text{13}}$ that of our Sun and acts like a single mass 2 Mly away? (b) What is the ratio of this force to the person’s weight? Note that Andromeda is the closest large galaxy.

Andromeda galaxy is the closest large galaxy and is visible to the naked eye. Estimate its brightness relative to the Sun, assuming it has luminosity ${\text{10}}^{\text{12}}$ times that of the Sun and lies 2 Mly away.

(a) A particle and its antiparticle are at rest relative to an observer and annihilate (completely destroying both masses), creating two $\gamma$ rays of equal energy. What is the characteristic $\gamma$ -ray energy you would look for if searching for evidence of proton-antiproton annihilation? (The fact that such radiation is rarely observed is evidence that there is very little antimatter in the universe.) (b) How does this compare with the 0.511-MeV energy associated with electron-positron annihilation?

The average particle energy needed to observe unification of forces is estimated to be ${\text{10}}^{\text{19}}\text{GeV}$ . (a) What is the rest mass in kilograms of a particle that has a rest mass of ${\text{10}}^{\text{19}}\text{GeV/}{c}^2$ ? (b) How many times the mass of a hydrogen atom is this?

The peak intensity of the CMBR occurs at a wavelength of 1.1 mm. (a) What is the energy in eV of a 1.1-mm photon? (b) There are approximately ${\text{10}}^9$ photons for each massive particle in deep space. Calculate the energy of ${\text{10}}^9$ such photons. (c) If the average massive particle in space has a mass half that of a proton, what energy would be created by converting its mass to energy? (d) Does this imply that space is “matter dominated”? Explain briefly.

(a) What Hubble constant corresponds to an approximate age of the universe of ${\text{10}}^{\text{10}}$ y? To get an approximate value, assume the expansion rate is constant and calculate the speed at which two galaxies must move apart to be separated by 1 Mly (present average galactic separation) in a time of ${\text{10}}^{\text{10}}$ y. (b) Similarly, what Hubble constant corresponds to a universe approximately $2\times {\text{10}}^{\text{10}}$ -y old?

Show that the velocity of a star orbiting its galaxy in a circular orbit is inversely proportional to the square root of its orbital radius, assuming the mass of the stars inside its orbit acts like a single mass at the center of the galaxy. You may use an equation from a previous chapter to support your conclusion, but you must justify its use and define all terms used.

The core of a star collapses during a supernova, forming a neutron star. Angular momentum of the core is conserved, and so the neutron star spins rapidly. If the initial core radius is $5\text{.}0\times {\text{10}}^5\text{km}$ and it collapses to 10.0 km, find the neutron star’s angular velocity in revolutions per second, given the core’s angular velocity was originally 1 revolution per 30.0 days.

Using data from the previous problem, find the increase in rotational kinetic energy, given the core’s mass is 1.3 times that of our Sun. Where does this increase in kinetic energy come from?

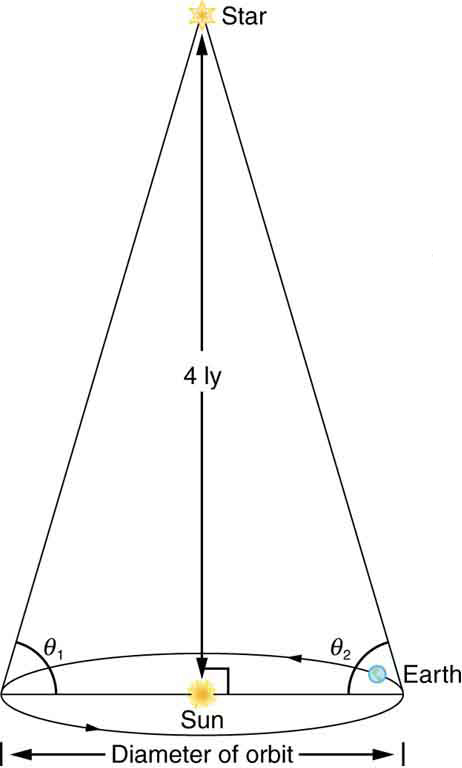
Distances to the nearest stars (up to 500 ly away) can be measured by a technique called parallax, as shown in [link] . What are the angles ${\theta }_1$ and ${\theta }_2$ relative to the plane of the Earth’s orbit for a star 4.0 ly directly above the Sun?

(a) Use the Heisenberg uncertainty principle to calculate the uncertainty in energy for a corresponding time interval of ${\text{10}}^{-\text{43}}\text{s}$ . (b) Compare this energy with the ${\text{10}}^{\text{19}}\text{GeV}$ unification-of-forces energy and discuss why they are similar.

Construct Your Own Problem

Consider a star moving in a circular orbit at the edge of a galaxy. Construct a problem in which you calculate the mass of that galaxy in kg and in multiples of the solar mass based on the velocity of the star and its distance from the center of the galaxy.