1. Home
  2. Une: physics for the health
  3. Unit 09a - circular motion
  4. Satellites and kepler’s laws:

10.5 Satellites and kepler’s laws: an argument for simplicity  (Page 2/5)

<< Chapter < Page
  Une: physics for the health     Page 2 / 5
Chapter >> Page >

Kepler’s Third Law

The ratio of the squares of the periods of any two planets about the Sun is equal to the ratio of the cubes of their average distances from the Sun. In equation form, this is

T 1  2 T 2  2 = r 1  3 r 2  3 , size 12{ { {T rSub { size 8{1} } rSup { size 8{2} } } over {T rSub { size 8{2} } rSup { size 8{2} } } } = { {r rSub { size 8{1} } rSup { size 8{3} } } over {r rSub { size 8{2} } rSup { size 8{3} } } } } {}

where T size 12{T} {} is the period (time for one orbit) and r size 12{r} {} is the average radius. This equation is valid only for comparing two small masses orbiting the same large one. Most importantly, this is a descriptive equation only, giving no information as to the cause of the equality.

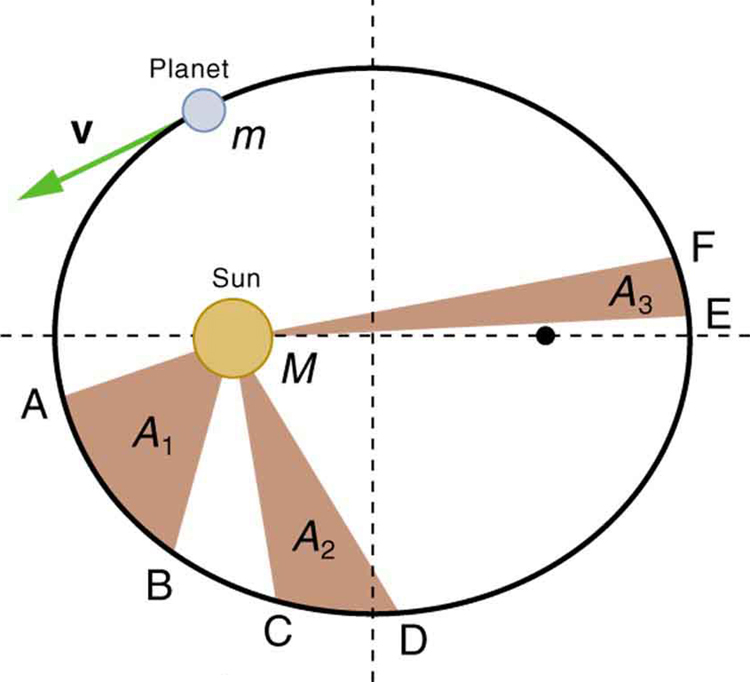
In the figure, the elliptical path of a planet is shown. The Sun is at the left focus. Three shaded regions M A B, M C D and M E F are marked on the figure by joining the Sun to the three pairs of points A B, C D, and E F on the elliptical path. The velocity of the planet is shown on the planet in a direction tangential to the path.
The shaded regions have equal areas. It takes equal times for m size 12{m} {} to go from A to B, from C to D, and from E to F. The mass m size 12{m} {} moves fastest when it is closest to M size 12{M} {} . Kepler’s second law was originally devised for planets orbiting the Sun, but it has broader validity.

Note again that while, for historical reasons, Kepler’s laws are stated for planets orbiting the Sun, they are actually valid for all bodies satisfying the two previously stated conditions.

Find the time for one orbit of an earth satellite

Given that the Moon orbits Earth each 27.3 d and that it is an average distance of 3.84 × 10 8 m size 12{3 "." "84" times "10" rSup { size 8{8} } m} {} from the center of Earth, calculate the period of an artificial satellite orbiting at an average altitude of 1500 km above Earth’s surface.

Strategy

The period, or time for one orbit, is related to the radius of the orbit by Kepler’s third law, given in mathematical form in T 1  2 T 2  2 = r 1  3 r 2  3 size 12{ { {T rSub { size 8{1} } rSup { size 8{2} } } over {T rSub { size 8{2} } rSup { size 8{2} } } } = { {r rSub { size 8{1} } rSup { size 8{3} } } over {r rSub { size 8{2} } rSup { size 8{3} } } } } {} . Let us use the subscript 1 for the Moon and the subscript 2 for the satellite. We are asked to find T 2 size 12{T rSub { size 8{2} } } {} . The given information tells us that the orbital radius of the Moon is r 1 = 3 . 84 × 10 8 m size 12{r rSub { size 8{1} } =3 "." "84" times "10" rSup { size 8{8} } m} {} , and that the period of the Moon is T 1 = 27.3 d size 12{T rSub { size 8{1} } ="27" "." 3} {} . The height of the artificial satellite above Earth’s surface is given, and so we must add the radius of Earth (6380 km) to get r 2 = ( 1500 + 6380 ) km = 7880 km size 12{r rSub { size 8{2} } = \( "1500"+"6380" \) "km"="7880"`"km"} {} . Now all quantities are known, and so T 2 size 12{T rSub { size 8{2} } } {} can be found.

Solution

Kepler’s third law is

T 1  2 T 2  2 = r 1  3 r 2  3 . size 12{ { {T rSub { size 8{1} } rSup { size 8{2} } } over {T rSub { size 8{2} } rSup { size 8{2} } } } = { {r rSub { size 8{1} } rSup { size 8{3} } } over {r rSub { size 8{2} } rSup { size 8{3} } } } } {}

To solve for T 2 size 12{T rSub { size 8{2} } } {} , we cross-multiply and take the square root, yielding

T 2  2 = T 1  2 r 2 r 1 3 size 12{T rSub { size 8{2} } =T rSub { size 8{1} } times left ( { {r rSub { size 8{2} } } over {r rSub { size 8{1} } } } right ) rSup { size 8{3/2} } } {}
T 2 = T 1 r 2 r 1 3 / 2 . size 12{T rSub { size 8{2} } =T rSub { size 8{1} } times left ( { {r rSub { size 8{2} } } over {r rSub { size 8{1} } } } right ) rSup { size 8{3/2} } } {}

Substituting known values yields

T 2 = 27.3 d × 24.0 h d × 7880 km 3.84 × 10 5 km 3 / 2 = 1.93 h.

Discussion This is a reasonable period for a satellite in a fairly low orbit. It is interesting that any satellite at this altitude will orbit in the same amount of time. This fact is related to the condition that the satellite’s mass is small compared with that of Earth.

People immediately search for deeper meaning when broadly applicable laws, like Kepler’s, are discovered. It was Newton who took the next giant step when he proposed the law of universal gravitation. While Kepler was able to discover what was happening, Newton discovered that gravitational force was the cause.

Derivation of kepler’s third law for circular orbits

We shall derive Kepler’s third law, starting with Newton’s laws of motion and his universal law of gravitation. The point is to demonstrate that the force of gravity is the cause for Kepler’s laws (although we will only derive the third one).

Let us consider a circular orbit of a small mass m size 12{m} {} around a large mass M size 12{m} {} , satisfying the two conditions stated at the beginning of this section. Gravity supplies the centripetal force to mass m size 12{m} {} . Starting with Newton’s second law applied to circular motion,
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Une: physics for the health professions. OpenStax CNX. Aug 20, 2014 Download for free at http://legacy.cnx.org/content/col11697/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Une: physics for the health professions' conversation and receive update notifications?

Ask