10.5 Pascal’s principle  (Page 2/3)

Relationship between forces in a hydraulic system

We can derive a relationship between the forces in the simple hydraulic system shown in [link] by applying Pascal’s principle. Note first that the two pistons in the system are at the same height, and so there will be no difference in pressure due to a difference in depth. Now the pressure due to $F_1$ acting on area $A_1$ is simply $P_1=\frac{F_1}{A_1}$ , as defined by $P=\frac{F}{A}$ . According to Pascal’s principle, this pressure is transmitted undiminished throughout the fluid and to all walls of the container. Thus, a pressure $P_2$ is felt at the other piston that is equal to $P_1$ . That is $P_1=P_2$ .

But since $P_2=\frac{F_2}{A_2}$ , we see that $\frac{F_1}{A_1}=\frac{F_2}{A_2}$ .

This equation relates the ratios of force to area in any hydraulic system, providing the pistons are at the same vertical height and that friction in the system is negligible. Hydraulic systems can increase or decrease the force applied to them. To make the force larger, the pressure is applied to a larger area. For example, if a 100-N force is applied to the left cylinder in [link] and the right one has an area five times greater, then the force out is 500 N. Hydraulic systems are analogous to simple levers, but they have the advantage that pressure can be sent through tortuously curved lines to several places at once.

Calculating force of slave cylinders: pascal puts on the brakes

Consider the automobile hydraulic system shown in [link] .

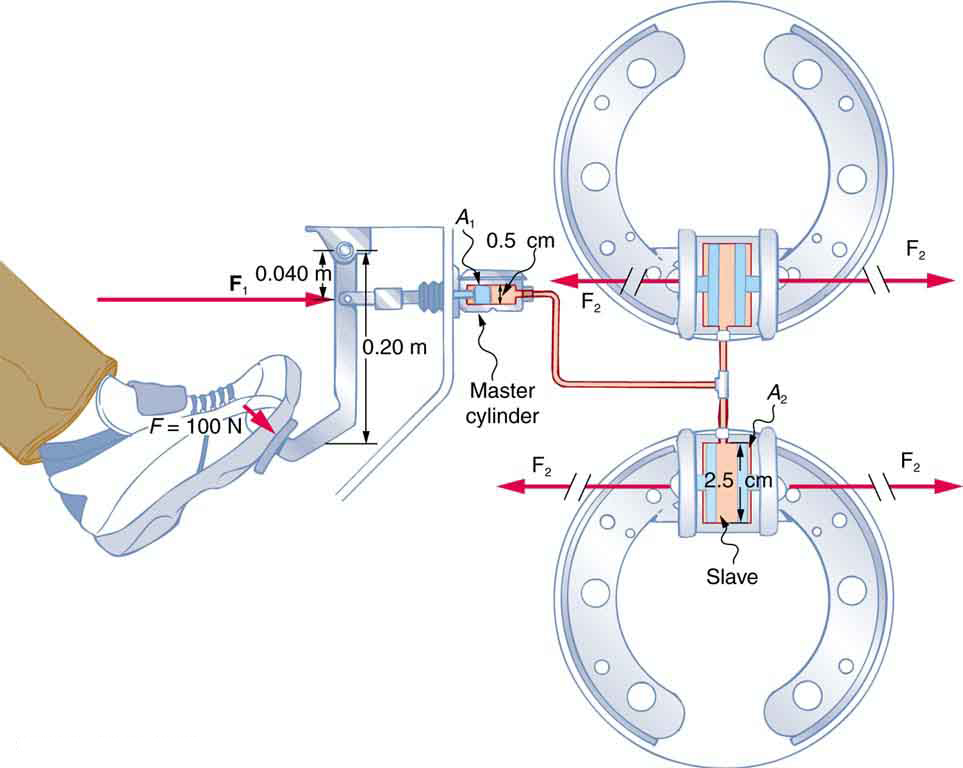
A force of 100 N is applied to the brake pedal, which acts on the cylinder—called the master—through a lever. A force of 500 N is exerted on the master cylinder. (The reader can verify that the force is 500 N using techniques of statics from Applications of Statics, Including Problem-Solving Strategies .) Pressure created in the master cylinder is transmitted to four so-called slave cylinders. The master cylinder has a diameter of 0.500 cm, and each slave cylinder has a diameter of 2.50 cm. Calculate the force $F_2$ created at each of the slave cylinders.

Strategy

We are given the force $F_1$ that is applied to the master cylinder. The cross-sectional areas $A_1$ and $A_2$ can be calculated from their given diameters. Then $\frac{F_1}{A_1}=\frac{F_2}{A_2}$ can be used to find the force $F_2$ . Manipulate this algebraically to get $F_2$ on one side and substitute known values:

Solution

Pascal’s principle applied to hydraulic systems is given by $\frac{F_1}{A_1}=\frac{F_2}{A_2}$ :

$F_2=\frac{A_2}{A_1}{F}_1=\frac{{\mathrm{\pi r}}_2^2}{{\mathrm{\pi r}}_1^2}{F}_1=\frac{{\left(\mathrm{1.25\; cm}\right)}^2}{{\left(\mathrm{0.250\; cm}\right)}^2}\times \text{500 N}=1\text{.}\text{25}\times {\text{10}}^4\text{N}.$

Discussion

This value is the force exerted by each of the four slave cylinders. Note that we can add as many slave cylinders as we wish. If each has a 2.50-cm diameter, each will exert $1\text{.}\text{25}\times {\text{10}}^4\text{N}\text{.}$

A simple hydraulic system, such as a simple machine, can increase force but cannot do more work than done on it. Work is force times distance moved, and the slave cylinder moves through a smaller distance than the master cylinder. Furthermore, the more slaves added, the smaller the distance each moves. Many hydraulic systems—such as power brakes and those in bulldozers—have a motorized pump that actually does most of the work in the system. The movement of the legs of a spider is achieved partly by hydraulics. Using hydraulics, a jumping spider can create a force that makes it capable of jumping 25 times its length!

Section summary

• Pressure is force per unit area.
• A change in pressure applied to an enclosed fluid is transmitted undiminished to all portions of the fluid and to the walls of its container.
• A hydraulic system is an enclosed fluid system used to exert forces.

Conceptual questions

Problems&Exercises