| << Chapter < Page | Chapter >> Page > |
In the exercise “Inverse of the Generic 2x2 Matrix,” you found that the inverse of the matrix is . This formula can be used to very quickly find the inverse of any 2x2 matrix.
Note that if , the formula does not work, since it puts a 0 in the denominator. This tells us that, for any 2x2 matrix, if the matrix has no inverse .
The quantity ad–bc is therefore seen to have a special importance for 2x2 matrices, and it is accorded a special name: the “determinant.” Determinants are represented mathematically with absolute value signs: the determinant of matrix [A] is |A|.
For instance, for the matrix , the determinant is (3)(6)–(4)(5) = –2.
Note that the determinant is a number , not a matrix. It is a special number that is associated with a matrix.
We said earlier that “if the matrix has no inverse .” We can now restate this result.
Any square matrix whose determinant is not 0, has an inverse matrix. Any square matrix with determinant 0 has no inverse.
This very important result is analogous to the result stated earlier for numbers: every number except 0 has an inverse.
Any square matrix has a determinant—an important number associated with that matrix. Non-square matrices do not have a determinant.
How do you find the determinant of a 3x3 matrix? The method presented here is referred to as “expansion by minors.” There are other methods, but they turn out to be mathematically equivalent to this one: that is, they end up doing the same arithmetic and arriving at the same answer.
| Example: Finding the Determinant of a 3x3 Matrix | |
|---|---|
| Find the determinant of | The problem. |
| ***SORRY, THIS MEDIA TYPE IS NOT SUPPORTED.*** | We’re going to walk through the top row, one element at a time, starting with the first element (the 2). In each case, begin by crossing out the row and column that contain that number. |
| =(8)(1)–(3)(1)=5 | Once you cross out one row and column, you are left with a 2x2 matrix (a “minor”). Take the determinant of that matrix. |
| 2(5)=10 | Now, that “minor” is what we got by crossing out a 2 in the top row. Multiply that number in the top row (2) by the determinant of the minor (5). |
| ***SORRY, THIS MEDIA TYPE IS NOT SUPPORTED.*** (10)(1)–(3)(1)= 74(7)=28 | Same operation for the second element in the row (the 4 in this case)... |
| ***SORRY, THIS MEDIA TYPE IS NOT SUPPORTED.*** (10)(1)–(8)(1) = 25(2)=10 | ...and the third (the 5 in this case). |
| +10 – 28 + 10 = –8 | Take these numbers, and alternately add and subtract them; add the first, subtract the second, add the third. The result of all that is the determinant. |
This entire process can be written more concisely as:
This method of “expansion of minors” can be extended upward to any higher-order square matrix. For instance, for a 4x4 matrix, each “minor” that is left when you cross out a row and column is a 3x3 matrix. To find the determinant of the 4x4, you have to find the determinants of all four 3x3 minors!
Fortunately, your calculator can also find determinants. Enter the matrix given above as matrix [D]. Then type:
MATRX ►
1
MATRX 4 ) ENTER
The screen should now look like this:
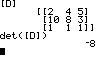
If you watched the calculator during that sequence, you saw that the right-arrow key took you to the
MATH submenu within the
MATRIX menus. The first item in that submenu is
DET ( which means “determinant of.”
What does the determinant mean? It turns out that this particular odd set of operations has a surprising number of applications. We have already seen one—in the case of a 2x2 matrix, the determinant is part of the inverse. And for any square matrix, the determinant tells you whether the matrix has an inverse at all.
Another application is for finding the area of triangles. To find the area of a triangle whose vertices are (a,b), (c,d), and (e,f), you can use the formula: Area = ½ . Hence, if you draw a triangle with vertices (2,10), (4,8), and (5,3), the above calculation shows that the area of this triangle will be 4.

Notification Switch
Would you like to follow the 'Advanced algebra ii: conceptual explanations' conversation and receive update notifications?