10.4 Doppler effect and sonic booms  (Page 2/9)

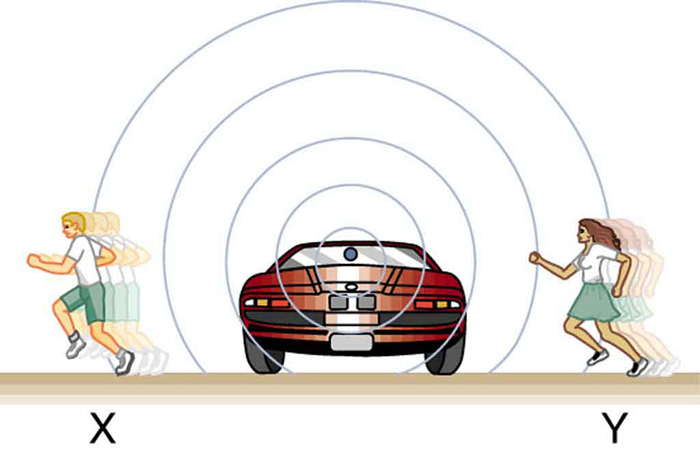
We know that wavelength and frequency are related by $v_{\mathrm{w}}=\mathrm{f\lambda }$ , where $v_{\mathrm{w}}$ is the fixed speed of sound. The sound moves in a medium and has the same speed $v_{\mathrm{w}}$ in that medium whether the source is moving or not. Thus $f$ multiplied by $\lambda$ is a constant. Because the observer on the right in [link] receives a shorter wavelength, the frequency she receives must be higher. Similarly, the observer on the left receives a longer wavelength, and hence he hears a lower frequency. The same thing happens in [link] . A higher frequency is received by the observer moving toward the source, and a lower frequency is received by an observer moving away from the source. In general, then, relative motion of source and observer toward one another increases the received frequency. Relative motion apart decreases frequency. The greater the relative speed is, the greater the effect.

For a stationary observer and a moving source, the frequency f _obs received by the observer can be shown to be

where $f_{\mathrm{s}}$ is the frequency of the source, $v_{\mathrm{s}}$ is the speed of the source along a line joining the source and observer, and $v_{\mathrm{w}}$ is the speed of sound. The minus sign is used for motion toward the observer and the plus sign for motion away from the observer, producing the appropriate shifts up and down in frequency. Note that the greater the speed of the source, the greater the effect. Similarly, for a stationary source and moving observer, the frequency received by the observer $f_{\text{obs}}$ is given by

where $v_{\text{obs}}$ is the speed of the observer along a line joining the source and observer. Here the plus sign is for motion toward the source, and the minus is for motion away from the source.

Calculate doppler shift: a train horn

Suppose a train that has a 150-Hz horn is moving at 35.0 m/s in still air on a day when the speed of sound is 340 m/s.

(a) What frequencies are observed by a stationary person at the side of the tracks as the train approaches and after it passes?

(b) What frequency is observed by the train’s engineer traveling on the train?

Strategy

To find the observed frequency in (a), $f_{\text{obs}}=f_{\mathrm{s}}\left(\frac{v_{\mathrm{w}}}{v_{\mathrm{w}}\pm v_{\mathrm{s}}}\right),$ must be used because the source is moving. The minus sign is used for the approaching train, and the plus sign for the receding train. In (b), there are two Doppler shifts—one for a moving source and the other for a moving observer.