| << Chapter < Page | Chapter >> Page > |
For the quadratic equations in the following problems, specify the values of and
( [link] )
( [link] )
For the following problems, use the zero-factor property to solve each quadratic equation.
( [link] )
( [link] )
( [link] )
For the following problems, solve each quadratic equation by factoring.
( [link] )
( [link] )
( [link] )
( [link] )
( [link] )
( [link] )
For the following problems, solve each quadratic equation by extraction of roots.
( [link] )
( [link] )
( [link] )
( [link] )
( [link] )
( [link] ) for
( [link] ) for
For the following problems, solve each quadratic equation using quadratic formula.
( [link] )
( [link] )
( [link] )
( [link] )
( [link] )
( [link] )
( [link] )
For the following problems, solve each quadratic equation by completing the square.
( [link] )
( [link] )
( [link] ) The product of two consecutive odd integers is 143. What are they?
11 and 13 or and
(
[link] ) A study of the air quality by an environmental group suggests that
years from now the level of carbon monoxide in the air, in parts per million, will be given by the quadratic equation
where
represents the amount of carbon monoxide in the air.
(a) What is the level, in parts per million, of carbon monoxide in the air now?
(b) How many years from now will the level of carbon monoxide be at18.1 parts per million?
(a) (b) 6 years from now
( [link] ) The length of a rectangle is 6 inches longer than the width of the rectangle. Find the dimensions of the rectangle if the area is 112 square feet.
For the following problems, construct the graphs of the following equations.
(
[link] )
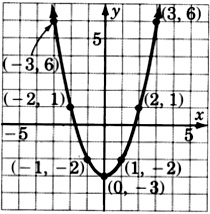
(
[link] )

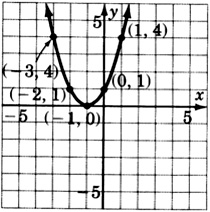
(
[link] )

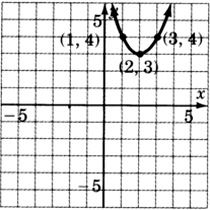
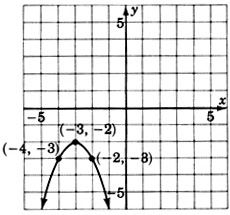
For the following problems, write the equation that corresponds to each graph.
(
[link] )
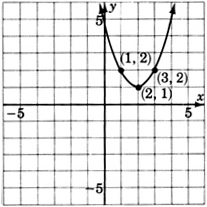
(
[link] )

Notification Switch
Would you like to follow the 'Basic mathematics review' conversation and receive update notifications?