1.8 Algebraic generalizations

When you have a “generalization,” you have one broad fact that allows you to assume many specific facts as examples.

If any one of the individual statements does not work, the generalization is invalid. (This generalization became problematic with the invention of the helium balloon.)

Scientists tend to work empirically, meaning they start with the specific facts and work their way back to the generalization. Generalizations are valued in science because they bring order to apparently disconnected facts, and that order in turn suggests underlying theories.

Mathematicians also spend a great deal of time looking for generalizations. When you have an “algebraic generalization” you have one algebraic fact that allows you to assume many numerical facts as examples.

Consider, for instance, the first two functions in the function game.

1. Double the number, then add six.
2. Add three to the number, then double.

These are very different “recipes.” However, their inclusion in the function game is a bit unfair, because—here comes the generalization— these two functions will always give the same answer. Whether the input is positive or negative, integer or fraction, small or large, these two functions will mimic each other perfectly. We can express this generalization in words.

There is literally an infinite number of specific claims that fit this pattern. We don’t need to prove or test each of these claims individually: once we have proven the generalization, we know that all these facts must be true.

We can express this same generalization pictorially by showing two “function machines” that always do the same thing.

$\begin{array}{c}-5\to \\ 0\to \\ \text{13}\to \end{array}$

$\begin{array}{c}\to 2(-5)+6=-4\\ \to 2(0)+6=6\\ \to 2(\text{13})+6=\text{32}\end{array}$

$\begin{array}{c}-5\to \\ 0\to \\ \text{13}\to \end{array}$

$\begin{array}{c}\to 2(-5)+6=-4\\ \to 2(0)+6=6\\ \to 2(\text{13})+6=\text{32}\end{array}$

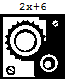But the most common way to express this generalization is algebraically, by asserting that these two functions equal each other.

Many beginning Algebra II students will recognize this as the distributive property. Given $2(x+3)$ they can correctly turn it into $\mathrm{2x}+6$ . But they often fail to realize what this equality means—that given the same input, the two functions will always yield the same output.

It’s worth stopping for a moment here to think about the $=$ symbol. Whenever it is used, $=$ indicates that two things are the same. However, the following two equations use the $=$ in very different ways.

In the first equation, the $=$ challenges you to solve for $x$ . “Find all the $x$ values that make this equation true.” The answers in this case are $x=\frac{1}{2}$ and $x=-3$ . If you plug in either of these two $x$ -values, you get a true equation; for any other $x$ -value, you get a false equation.

The second equation cannot be solved for $x$ ; the $=$ sign in this case is asserting an equality that is true for any $x$ -value. Let’s try a few.

With a calculator, you can attempt more difficult values such as $x=-\text{26}$ or $x=\pi$ ; in every case, the two formulas will give the same answer. When we assert that two very different functions will always produce the same answers, we are making a very powerful generalization.

Exception : $x=-3$ is outside the domain of one of these two functions. In this important sense, the two functions are not in fact equal. Take a moment to make sure you understand why this is true!

Such generalizations are very important because they allow us to simplify .

Suppose that you were told “I am going to give you a hundred numbers. For each number I give you, square it, then double the answer, then subtract eighteen, then divide by the original number plus three.” This kind of operation comes up all the time. But you would be quite relieved to discover that you can accomplish the same task by simply doubling each number and subtracting 6! The generalization in this case is $\frac{{\mathrm{2x}}^2-\text{18}}{x+3}=\mathrm{2x}-6$ ; you will be creating exactly this sort of generalization in the chapter on Rational Expressions.