| << Chapter < Page | Chapter >> Page > |
Maak baie seker dat die leerders nie die voorste getal van ‘n aftrekbewerking herbenoem nie. ( Dit is die rede waarom hulle later probleme ondervind as hulle ‘n bewerking waar ‘n groep van 10 ontbind moet word, kry. )
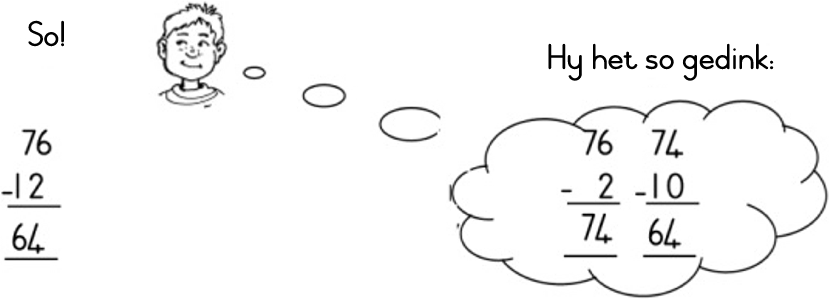
Voorbeeld: 76 - 12 = ______
Probeer dit!
Gooi 76 tellers, wat in tiene en ene gegroepeer is, in ‘n plastieksak.
Laat ‘n leerder nou 2 kom uithaal.
Vra : Hoeveel is in die sak oor? 74
Wat is gedoen? ( 2 ene is uitgehaal) Skryf : 76 - 2 = 74
Laat ‘n ander leerder nou die 10 kom uithaal.
Vra : Wat is nou oor in die sak? 64
Wat is gedoen? ( 1 tien is uitgehaal) Skryf : 74 - 10 = 64
Om te toets, word eers 10 en dan 2 weer terug in die sak gegooi. Nou is daar weer 76 .
Onthou : Alle bewerkings word nog sonder oordrag of ontbinding van ‘n tien gedoen.
Leerders kan horisontaal of vertikaal werk. Dit is hulle keuse.
Help die leerders net om aan die gang te kom met die ontsyfering van die geheime kode. Hulle moet net begryp dat elke teken ‘n letter van die alfabet voorstel. Los hulle dan om self te probeer.
Moedig almal aan om iets met die kode te skryf, al is dit net hul eie naam.
Dit is ook ‘n geleentheid om uit te vind wie reeds die alfabet ken. Dalk kan dit sommer dien as aansporing om dit te leer.
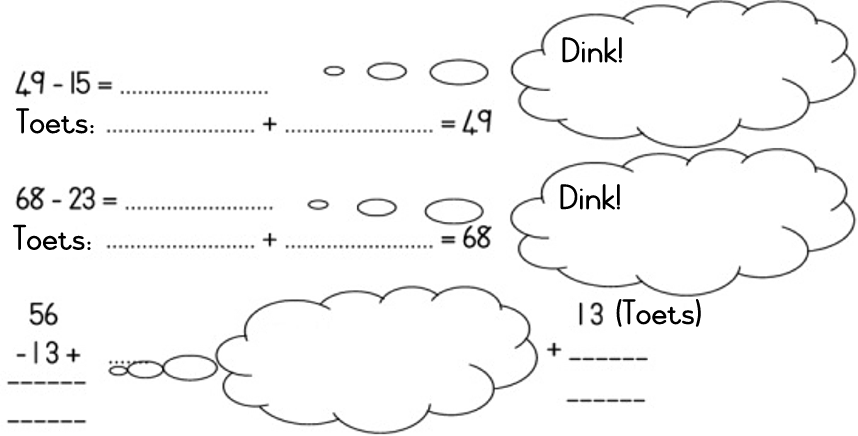
Ek skat ____________________________________________________________
Skryf : Ek het ___________________________________________ geskat.
Met hoeveel is jy uit?_____________________________________________
Skryf : My getal is ___________________________________________________
Skryf : Ek kan _______________bytel: ____________ + ____________ = 50
Skryf : Ek kan _______________ wegneem: : __________ - __________ = 40
| LU 1.8 |
Om 'n getal te kan afrond tot die naaste tien , moet jy weet watter veelvoud van tien die naaste aan die getal is. As dit ewe ver is, gebruik ons die groter veelvoud van tien.
| 43 | 40 | 50 |
| 49 | 40 | 50 |
| 46 | 40 | 50 |
| 41 | 40 | 50 |
| LU 1.10 |
Onthou : As die ene 5 of meer as 5 is, gebruik ons die groter veelvoud .
24: naaste veelvoud is 20 16: naaste veelvoud is 20
37: naaste veelvoud is _____ 52: naaste veelvoud is _____
15: naaste veelvoud is _____ 73: naaste veelvoud is _____
81: naaste veelvoud is _____ 94: naaste veelvoud is _____
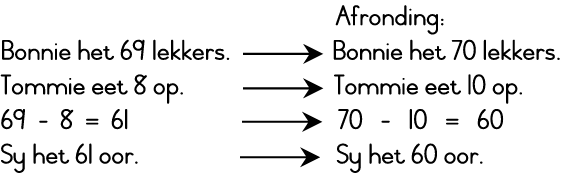
As ons afrond, help dit ons om vinniger te kan skat in watter omgewing die antwoord behoort te wees. Onthou! Dit is nie 'n akkurate antwoord nie!
Hoeveel geld het hy oor?
Afronding: Getalsin: _____________________________________________________________________
Bewerking: Getalsin: _____________________________________________________________________
Op dié manier kan 'n mens vinnig bereken hoeveel kleingeld jy min of meer moet kry as jy iets betaal en kleingeld moet kry.
| LU 1.10 |
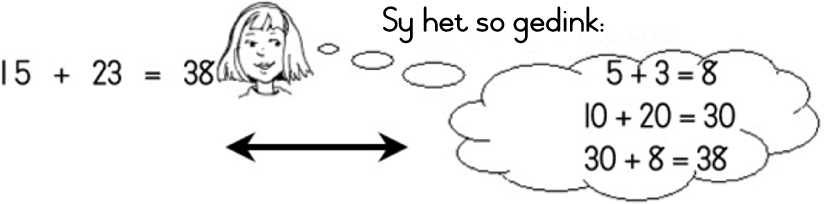
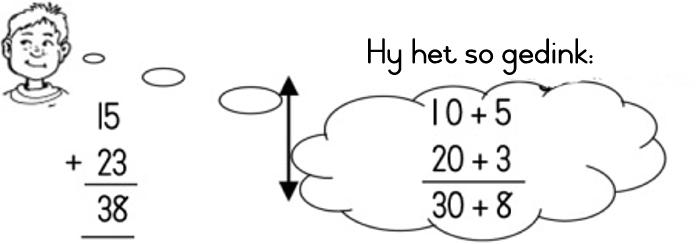
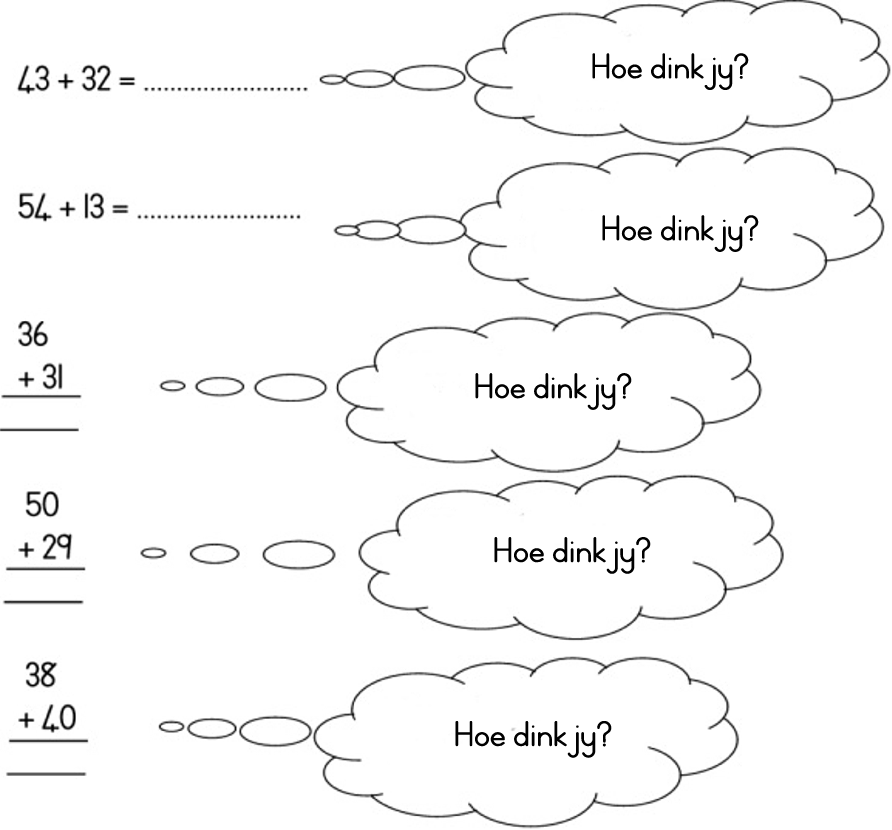
| LU 1.8 |
Bonnie sê: Die aftrekbewerking is 'n bietjie anders.

1 2
+64
76
_____________________________________________________________________
| LU 1.8 |
Leeruitkomste 1: Die leerder is in staat om getalle en die verwantskappe daarvan te herken, te beskryf en voor te stel, en om tydens probleemoplossing bevoeg en met selfvertroue te tel, te skat, te bereken en te kontroleer.
Assesseringstandaard 1.8: Dit is duidelik wanneer die leerder die gepaste simbole in berekeninge kan gebruik om probleme wat die volgende behels, op te los;
1.8.1 optelling en aftrekking van heelgetalle met minstens 3 syfers;
1.8.2 vermenigvuldiging van minstens 2-syferheelgetalle met 1-syferheelgetalle;
1.8.3 deling van minstens 2-syferheelgetalle deur 1-syferheelgetalle;
1.8.4 skatting;
Assesseringstandaard 1.10: Dit is duidelik wanneer die leerder die volgende tegnieke gebruik:
1.10.1 opbou en afbreek van getalle;
1.10.2 verdubbeling en halvering;
1.10.3 getallelyne;
1.10.4 afronding in tiene.

Notification Switch
Would you like to follow the 'Wiskunde graad 3' conversation and receive update notifications?