| << Chapter < Page | Chapter >> Page > |
Hierna kan dit skriftelik gedoen word.
Moedig hulle aan om gereeld te toets en later sal hulle dit outomaties doen.
Hulle tel sommer so van agter of van onder weer bymekaar.
Gebruik konkrete voorwerpe en help die leerders om self te ontdek wat ‘n ewe en ‘n onewe getal is. Doen dit net eers tot die getal 9.
Help hulle om die patroon van 11 tot 19 te ontdek.
Wanneer hulle die patroon van 2 4 6 8 0 aan die ene-kant vir ewe getalle en 1 3 5 7 9 aan die ene-kant vir onewe getalle ontdek, sal dit vir hulle lekker wees om dit op groot getalle toe te pas.
Die tekens =,<en>moet aangeleer word. Daarna kan die take in die module vervat, gedoen word. Gee nog soortgelyke take.
Leerders moet die woorde horisontaal en vertikaal ken en weet wat dit beteken.
Maak seker dat die leerders die nul (0) as plekhouer by die getalle sonder ene , soos 10, 20, 30, 40 ens. verstaan. Dit is veral belangrik by vertikale bewerkings.
Met die aanleer van vermenigvuldigingstafels is dit baie belangrik dat u by die metode waaraan die leerders gewoond is, sal bly.
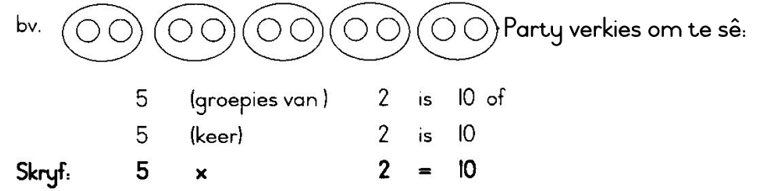
Ander verkies om te sê:
2 word 5 keer bymekaar getel. Dit is: 2 vermenigvuldig met 5 is 10
Skryf: 2 x 5 = 10
Sodra die leerders die kommutatiewe eienskap van vermenigvuldig
( 2 x 5 = 10 en 5 x 2 = 10) ontdek, is die skryfwyse nie so belangrik nie.
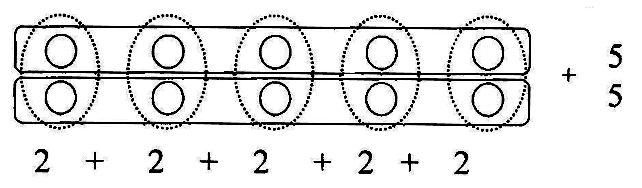
Moedig die leerders aan om hul denke in die “ wolkie ” op die bladsy aan te dui. Dit sal help om uit te vind hoe hulle dink en redeneer en waar hulle foute begaan.
As u as opvoeder nie halvering net na verdubbeling wil doen nie, los dit eers en doen dit later. Maak egter baie seker dat veral die stadiger leerders die proses van verdubbeling verstaan en baasgeraak het voordat halvering gedoen word. Doen ook eers net halvering van ewe getalle.
Dit is belangrik dat die leerders sal weet 10 2 kan 2 verskillende betekenisse hê: verdeling of groepering .
Kyk na die volgende 2 probleme:

Die getalsin is dieselfde, maar die voorstelling verskil.
Tel gereeld in tiene, aan en terug, vanaf enige getal.
Bv. 4 14 24 34 44 54 64 74 84 94
97 87 77 67 57 47 37 27 17 7
Leerders moet bewus wees van hoe belangrik die getal 10 in ons getalstelsel ( desimalestelsel ) is.
Hulle moet die kombinasies van 10 baie goed ken en hulle moet gereeld getoets word. Baie oefening is nodig.
Dit is baie belangrik dat die opvoeder voor die tyd die hopies tellers, ‘n getal tussen 40 en 50 , gereed sal hê om aan die leerders uit te deel, anders beteken die aktiwiteit niks.
Die skatting kan by u op die mat of by die banke gedoen word. Hulle sal miskien heeltemal te veel of te min skat, maar dit maak nie saak nie, want die werk wat volg, gaan oor die getal wat hulle werklik het.
Heelwat soortgelyke take mag nodig wees om veral die stadiger leerders te help om afronding te verstaan en baas te raak. Konkrete werk en herhaling is belangrik.
Verduidelik:
5 of meer as 5 ene, ---- rond af na die groter veelvoud van 10.
4 of minder as 4 ene, ---- rond af na die kleiner veelvoud van 10.
Die opvoeder moet die leerders help om die denkprosesse by die verskillende bewerkings te verstaan. Baie konkrete werk op die mat moet alle geskrewe werk voorafgaan. Gee die leerders geleentheid om te vertel hoe hulle dink en redeneer en wat hulle doen.

Notification Switch
Would you like to follow the 'Wiskunde graad 3' conversation and receive update notifications?