1.6 Lập trình cấu trúc dữ liệu và giải thuật  (Page 11/46)

Để cài đặt các thuật giải theo kiểu tìm kiếm BFS, người ta thường cần dùng 2 tập hợp sau :

OPEN : tập chứa các trạng thái đã được sinh ra nhưng chưa được xét đến (vì ta đã chọn một trạng thái khác). Thực ra, OPEN là một loại hàng đợi ưu tiên (priority queue) mà trong đó, phần tử có độ ưu tiên cao nhất là phần tử tốt nhất. Người ta thường cài đặt hàng đợi ưu tiên bằng Heap. Các bạn có thể tham khảo thêm trong các tài liệu về Cấu trúc dữ liệu về loại dữ liệu này.

CLOSE : tập chứa các trạng thái đã được xét đến. Chúng ta cần lưu trữ những trạng thái này trong bộ nhớ để đề phòng trường hợp khi một trạng thái mới được tạo ra lại trùng với một trạng thái mà ta đã xét đến trước đó. Trong trường hợp không gian tìm kiếm có dạng cây thì không cần dùng tập này.

Thuật giải BEST-FIRST SEARCH

1. Đặt OPEN chứa trạng thái khởi đầu.

2. Cho đến khi tìm được trạng thái đích hoặc không còn nút nào trong OPEN, thực hiện :

2.a. Chọn trạng thái tốt nhất (Tmax) trong OPEN (và xóa Tmax khỏi OPEN)

2.b. Nếu Tmax là trạng thái kết thúc thì thoát.

2.c. Ngược lại, tạo ra các trạng thái kế tiếp Tk có thể có từ trạng thái Tmax. Đối với mỗi trạng thái kế tiếp Tk thực hiện :

Tính f(Tk); Thêm Tk vào OPEN

BFS khá đơn giản. Tuy vậy, trên thực tế, cũng như tìm kiếm chiều sâu và chiều rộng, hiếm khi ta dùng BFS một cách trực tiếp. Thông thường, người ta thường dùng các phiên bản của BFS là AT, AKT và A*

Thông tin về quá khứ và tương lai

Thông thường, trong các phương án tìm kiếm theo kiểu BFS, độ tốt f của một trạng thái được tính dựa theo 2 hai giá trị mà ta gọi là là g và h’. h’ chúng ta đã biết, đó là một ước lượng về chi phí từ trạng thái hiện hành cho đến trạng thái đích (thông tin tương lai). Còn g là "chiều dài quãng đường" đã đi từ trạng thái ban đầu cho đến trạng thái hiện tại (thông tin quá khứ). Lưu ý rằng g là chi phí thực sự (không phải chi phí ước lượng). Để dễ hiểu, bạn hãy quan sát hình sau :

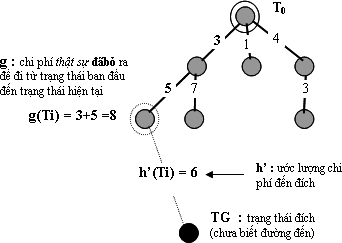
Hình 6.14 Phân biệt khái niệm g và h’

Kết hợp g và h’ thành f’ (f’ = g + h’) sẽ thể hiện một ước lượng về "tổng chi phí" cho con đường từ trạng thái bắt đầu đến trạng thái kết thúc dọc theo con đường đi qua trạng thái hiện hành. Để thuận tiện cho thuật giải, ta quy ước là g và h’ đều không âm và càng nhỏ nghĩa là càng tốt.

III.5. Thuật giải AT

Thuật giải AT là một phương pháp tìm kiếm theo kiểu BFS với độ tốt của nút là giá trị hàm g – tổng chiều dài con đường đã đi từ trạng thái bắt đầu đến trạng thái hiện tại.

Thuật giải AT

1. Đặt OPEN chứa trạng thái khởi đầu.

2. Cho đến khi tìm được trạng thái đích hoặc không còn nút nào trong OPEN, thực hiện :

2.a. Chọn trạng thái (Tmax) có giá trị g nhỏ nhất trong OPEN (và xóa Tmax khỏi OPEN)

2.b. Nếu Tmax là trạng thái kết thúc thì thoát.

2.c. Ngược lại, tạo ra các trạng thái kế tiếp Tk có thể có từ trạng thái Tmax. Đối với mỗi trạng thái kế tiếp Tk thực hiện :

g(Tk) = g(Tmax) + cost(Tmax, Tk);

Thêm Tk vào OPEN.

* Vì chỉ sử dụng hàm g (mà không dùng hàm ước lượng h’) fsđể đánh giá độ tốt của một trạng thái nên ta cũng có thể xem AT chỉ là một thuật toán.

III.6. Thuật giải AKT