| << Chapter < Page | Chapter >> Page > |
We would repeat the process until there are no more digits in the dividend to bring down. In this problem, there are no more digits to bring down, so the division is finished.
Check by multiplying the quotient times the divisor to get the dividend. Multiply to make sure that product equals the dividend,
It does, so our answer is correct.
Divide Check by multiplying:
| Let's rewrite the problem to set it up for long division. |
|
| Divide the first digit of the dividend, 2, by the divisor, 4. |
|
| Since 4 does not go into 2, we use the first two digits of the dividend and divide 25 by 4. The divisor 4 goes into 25 six times. | |
| We write the 6 in the quotient above the 5. |
|
| Multiply the 6 in the quotient by the divisor 4 and write the product, 24, under the first two digits in the dividend. |
 |
| Subtract that product from the first two digits in the dividend. Subtract . Write the difference, 1, under the second digit in the dividend. |
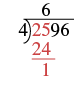 |
| Now bring down the 9 and repeat these steps. There are 4 fours in 19. Write the 4 over the 9. Multiply the 4 by 4 and subtract this product from 19. |
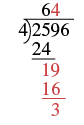 |
| Bring down the 6 and repeat these steps. There are 9 fours in 36. Write the 9 over the 6. Multiply the 9 by 4 and subtract this product from 36. |
 |
| So . | |
Check by multiplying.
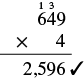 |
It equals the dividend, so our answer is correct.
Divide Check by multiplying:
| Let's rewrite the problem to set it up for long division. |
|
| First we try to divide 6 into 4. |
|
| Since that won't work, we try 6 into 45.
There are 7 sixes in 45. We write the 7 over the 5. |
|
| Multiply the 7 by 6 and subtract this product from 45. |
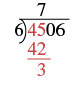 |
| Now bring down the 0 and repeat these steps. There are 5 sixes in 30.
Write the 5 over the 0. Multiply the 5 by 6 and subtract this product from 30. |
 |
| Now bring down the 6 and repeat these steps. There is 1 six in 6.
Write the 1 over the 6. Multiply 1 by 6 and subtract this product from 6. |
 |
Check by multiplying.
 |
It equals the dividend, so our answer is correct.
Divide Check by multiplying.
| Let's rewrite the problem to set it up for long division. |
|
| First we try to divide 9 into 7. |
|
| Since that won't work, we try 9 into 72. There are 8 nines in 72.
We write the 8 over the 2. |
|
| Multiply the 8 by 9 and subtract this product from 72. |
 |
| Now bring down the 6 and repeat these steps. There are 0 nines in 6.
Write the 0 over the 6. Multiply the 0 by 9 and subtract this product from 6. |
 |
| Now bring down the 3 and repeat these steps. There are 7 nines in 63. Write the 7 over the 3.
Multiply the 7 by 9 and subtract this product from 63. |
 |
Check by multiplying.
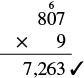 |
It equals the dividend, so our answer is correct.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?