| << Chapter < Page | Chapter >> Page > |
Given a function and both a vertical and a horizontal shift, sketch the graph.
Given sketch a graph of
The function is our toolkit absolute value function. We know that this graph has a V shape, with the point at the origin. The graph of has transformed in two ways: is a change on the inside of the function, giving a horizontal shift left by 1, and the subtraction by 3 in is a change to the outside of the function, giving a vertical shift down by 3. The transformation of the graph is illustrated in [link] .
Let us follow one point of the graph of
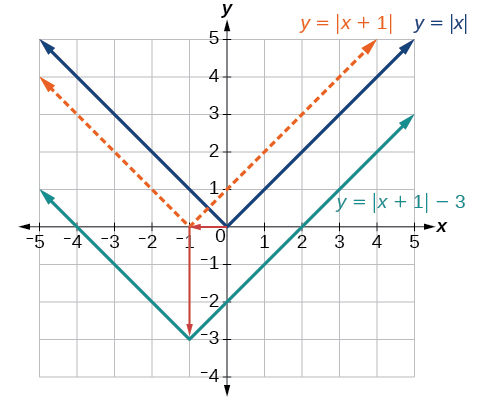
[link] shows the graph of
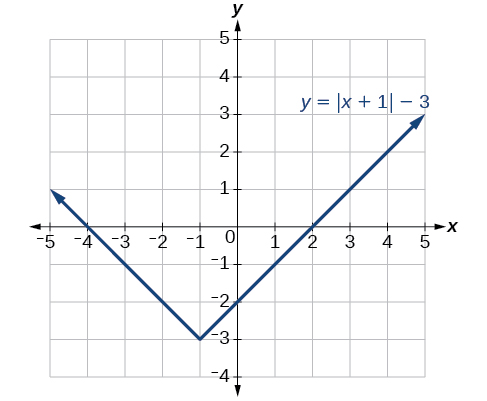
Given sketch a graph of
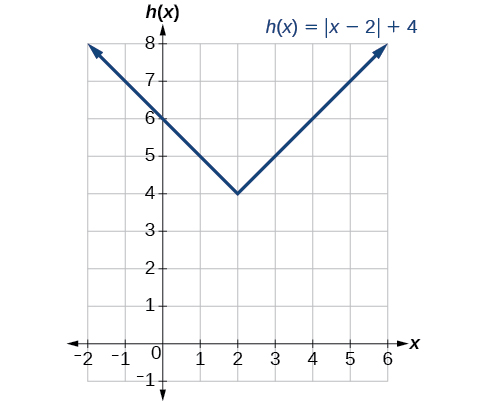
Write a formula for the graph shown in [link] , which is a transformation of the toolkit square root function.
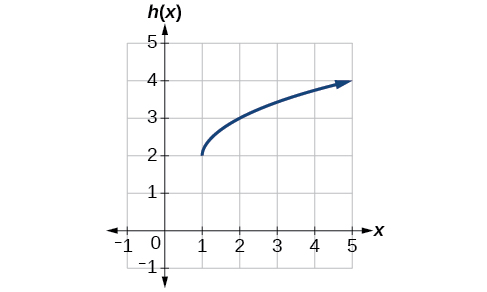
The graph of the toolkit function starts at the origin, so this graph has been shifted 1 to the right and up 2. In function notation, we could write that as
Using the formula for the square root function, we can write
Write a formula for a transformation of the toolkit reciprocal function that shifts the function’s graph one unit to the right and one unit up.
Another transformation that can be applied to a function is a reflection over the x - or y -axis. A vertical reflection reflects a graph vertically across the x -axis, while a horizontal reflection reflects a graph horizontally across the y -axis. The reflections are shown in [link] .
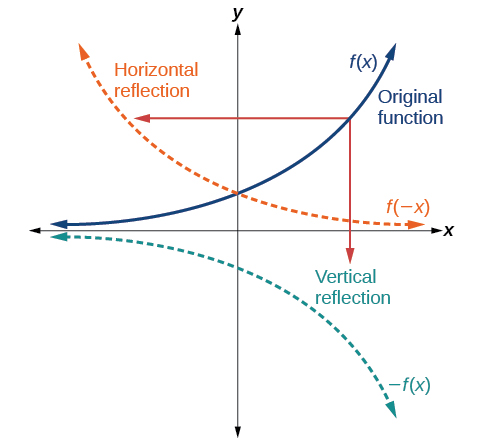
Notice that the vertical reflection produces a new graph that is a mirror image of the base or original graph about the x -axis. The horizontal reflection produces a new graph that is a mirror image of the base or original graph about the y -axis.
Given a function a new function is a vertical reflection of the function sometimes called a reflection about (or over, or through) the x -axis.
Given a function a new function is a horizontal reflection of the function sometimes called a reflection about the y -axis.
Given a function, reflect the graph both vertically and horizontally.

Notification Switch
Would you like to follow the 'Essential precalculus, part 1' conversation and receive update notifications?