1.4 The simple pendulum  (Page 30/3)

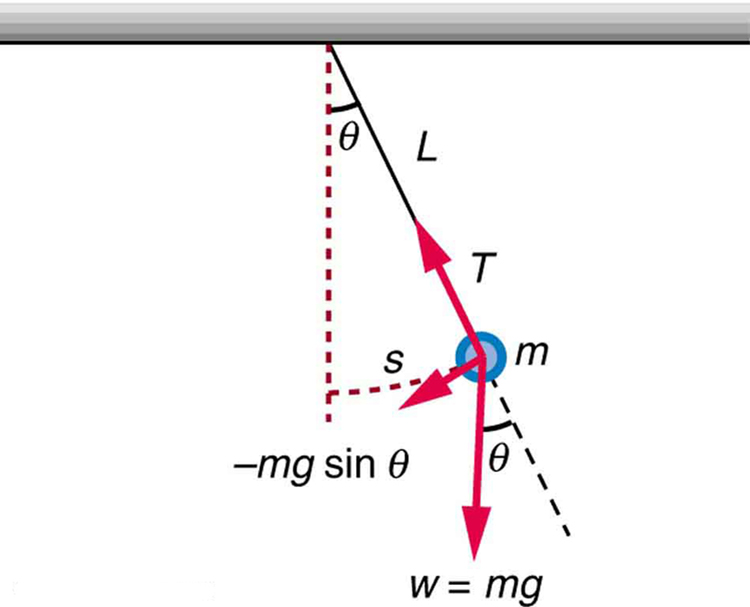
Pendulums are in common usage. Some have crucial uses, such as in clocks; some are for fun, such as a child’s swing; and some are just there, such as the sinker on a fishing line. For small displacements, a pendulum is a simple harmonic oscillator. A simple pendulum    is defined to have an object that has a small mass, also known as the pendulum bob, which is suspended from a light wire or string, such as shown in [link] . Exploring the simple pendulum a bit further, we can discover the conditions under which it performs simple harmonic motion, and we can derive an interesting expression for its period.

We begin by defining the displacement to be the arc length $s$ . We see from [link] that the net force on the bob is tangent to the arc and equals $-\text{mg}\text{sin}\theta$ . (The weight $\text{mg}$ has components $\text{mg}\text{cos}\theta$ along the string and $\text{mg}\text{sin}\theta$ tangent to the arc.) Tension in the string exactly cancels the component $\text{mg}\text{cos}\theta$ parallel to the string. This leaves a net restoring force back toward the equilibrium position at $\theta =0$ .

Now, if we can show that the restoring force is directly proportional to the displacement, then we have a simple harmonic oscillator. In trying to determine if we have a simple harmonic oscillator, we should note that for small angles (less than about $\text{15º}$ ), $\text{sin}\theta \approx \theta$ ( $\text{sin}\theta$ and $\theta$ differ by about 1% or less at smaller angles). Thus, for angles less than about $\text{15º}$ , the restoring force $F$ is

The displacement $s$ is directly proportional to $\theta$ . When $\theta$ is expressed in radians, the arc length in a circle is related to its radius ( $L$ in this instance) by:

so that

For small angles, then, the expression for the restoring force is:

This expression is of the form:

where the force constant is given by $k=\text{mg}/L$ and the displacement is given by $x=s$ . For angles less than about $\text{15º}$ , the restoring force is directly proportional to the displacement, and the simple pendulum is a simple harmonic oscillator.

Using this equation, we can find the period of a pendulum for amplitudes less than about $\text{15º}$ . For the simple pendulum:

Thus,

for the period of a simple pendulum. This result is interesting because of its simplicity. The only things that affect the period of a simple pendulum are its length and the acceleration due to gravity. The period is completely independent of other factors, such as mass. As with simple harmonic oscillators, the period $T$ for a pendulum is nearly independent of amplitude, especially if $\theta$ is less than about $\text{15º}$ . Even simple pendulum clocks can be finely adjusted and accurate.

Note the dependence of $T$ on $g$ . If the length of a pendulum is precisely known, it can actually be used to measure the acceleration due to gravity. Consider the following example.