| << Chapter < Page | Chapter >> Page > |
Given trigonometric functions of a special angle, evaluate using side lengths.
Find the exact value of the trigonometric functions of using side lengths.
Find the exact value of the trigonometric functions of using side lengths.
If we look more closely at the relationship between the sine and cosine of the special angles relative to the unit circle, we will notice a pattern. In a right triangle with angles of and we see that the sine of namely is also the cosine of while the sine of namely is also the cosine of
See [link]
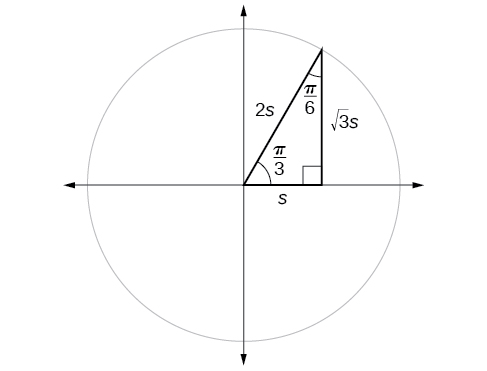
This result should not be surprising because, as we see from [link] , the side opposite the angle of is also the side adjacent to so and are exactly the same ratio of the same two sides, and Similarly, and are also the same ratio using the same two sides, and
The interrelationship between the sines and cosines of and also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to and the right angle is the remaining two angles must also add up to That means that a right triangle can be formed with any two angles that add to —in other words, any two complementary angles. So we may state a cofunction identity : If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in [link] .
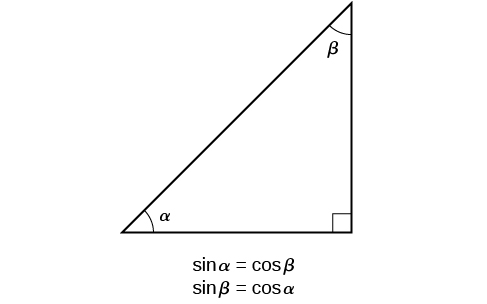
Using this identity, we can state without calculating, for instance, that the sine of equals the cosine of and that the sine of equals the cosine of We can also state that if, for a certain angle then as well.
Given the sine and cosine of an angle, find the sine or cosine of its complement.
If find
According to the cofunction identities for sine and cosine,
So
If find
2

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?