1.4 Results

Accurate detection of apogee

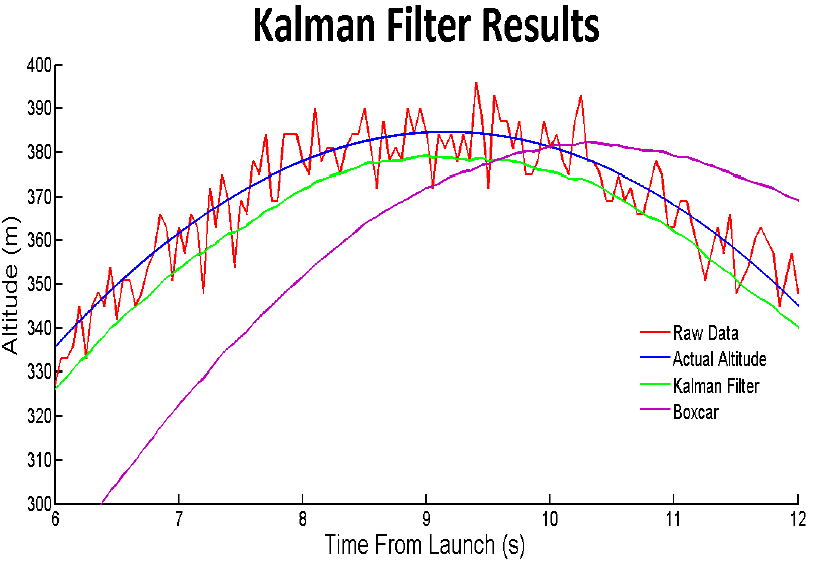
Because the Kalman filter takes the physical model of a noisy system into account, it was more effective at predicting states of a system than other commonly used filters. While other filters rely only on current and past states, the Kalman filter's ability to estimate future states mitigate the delay and error which make it superior to other common solutions. In particular, with respect to our rocket flight, we compared the effectiveness of the Kalman filter with the other filter that successfully smoothed the signal, the Boxcar filter. As [link] shows, the Kalman filter has significantly less delay, almost matching the actual apogee line in shape, than the filtered output of a Boxcar filter.

The Kalman filter does a remarkable job of removing noise from the position signal, but in order to actually determine apogee a decision rule is needed. Originally, the plan was to determine that the rocket was at apogee when its velocity was equal to zero. However, despite the fact that the accelerometer had very low variance compared to the barometer (which weighted it heavily in the Kalman gain), it had a significant bias term in it, which made the velocity term reach zero about a second before actual apogee. A more effective decision rule was to look for the position to have negative slope for three consecutive samples. Thus, apogee was defined as the time when the , position term was less than the previous position term, which in turn was less than the position term before that.

While the output of the Kalman filter has a negative amplitude bias compared when compared to actual apogee, it still accurately predicted the time of apogee, which is key to parachute deployment and minimizing forces on the rocket airframe and parachute.

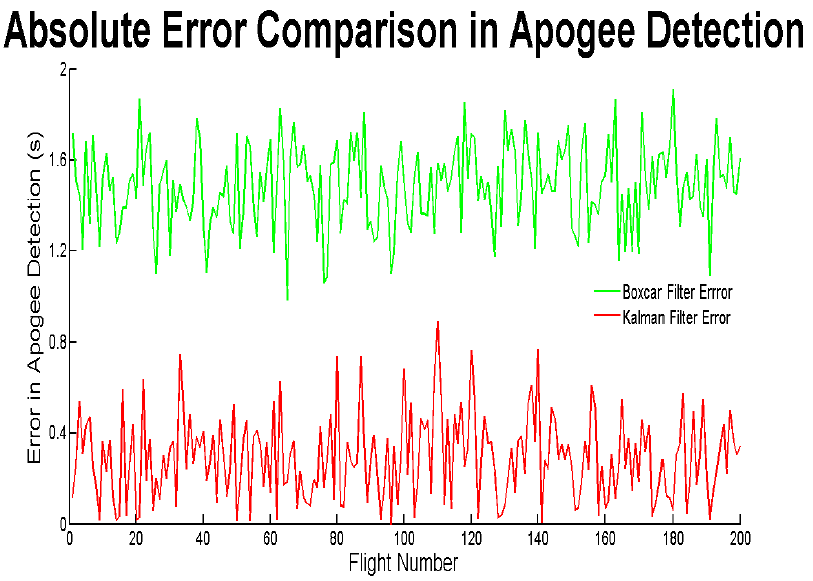
[link] makes the effectiveness of the Kalman filter even clearer. Across 200 flights with randomized parameters, the Kalman filter displayed a mean error in detecting apogee of 0.269 seconds while the Boxcar filter has a mean error of 1.52 seconds. In terms of velocity, the Kalman filter, on average, mitigates the velocity experienced by the rocket to 2.64 m/s, as opposed to the 14.9 m/s when a Boxcar filter is used. Effectively, the Kalman filter is about six times more accurate at determining apogee.