1.4 Graphing

Make sure, on the homework, that they reached something like $(x-a)(x+a)=x^2-a^2$ . Of course, someone may have used completely different letters; and someone else may have said that $(x-a)(x+a)+a^2=x^2$ . Point out that these are just as good—they look different, but they say the same thing. Finally, show them how they could have arrived at $(x-a)(x+a)=x^2-a^2$ through FOIL.

Once all questions are satisfied, on to graphing. This may actually be two days worth of material. Don’t rush it! And once again, no in-class assignment, but a lot of interaction.

Start by putting the following points on the board: (6,5)(3,6)(2,9)(5,7)(1,10)(4,8). Ask for a general description—if these represent the number of pushups you do each day, what’s the trend? Then graph them, and you can see a definite downward trend with an odd spike in the middle. Moral: we can see things in shapes that we can’t see in numbers .

Now, let’s jump to the idea of graphing functions. Draw a U-shape, the equation $f\left(x\right)=x^2$ , and say “This drawing is the graph of that function—but what does that mean ? What does this drawing actually have to do with that function?” Get to the point where the following ideas have come out. Every time you “do” the function, one number goes in and another comes out. When we graph it, the “in” function is always $x$ , and the “out” function is always $y$ —in other words, every time we graph a function, we are always graphing $y=f\left(x\right)$ . To put it another way, we are graphing all the points that have this particular relationship to each other. (Take as much time as you need on this point.)

Have the students graph $\left|x\right|$ (individually at their desks) by plotting points. This is not intended to teach them about absolute value, but to reinforce the ideas I just made about what it means to graph a function.

What can we tell by looking at a graph? Draw the graphs of $x^2$ and $x^3$ on the board. Talk about the things we can tell about these two functions by looking at the graphs . They both have one zero; they are similar on the right, except that $x^3$ rises faster; they are completely different on the left; they both have unlimited domains, but only one has an unlimited range. (Make sure to connect this back to “domain” and “range” from the function game!)

Now, draw this on the board.

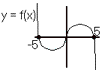
Time for another…brainstorming exercise! (Remind them that the object is quantity, not quality!) Each pair of students has to list as many things as it can tell about this function $f\left(x\right)$ by looking at the graph. Key points I want to bring out are:

• The three zeros. (Talk about the word “zeros.”)
• Places where the function is negative and places where it is positive.
• Places where it is increasing and places where it is decreasing. (Talk about slope!)
• What happens for very low and very high values of $x$ .
• For the experts, odd symmetry: $f(-x)=-f\left(x\right)$ .

Talk more about domain and range. This is unrestricted in both. We saw that $x^2$ has an unrestricted domain, but a restricted range. Why would any function have a limited domain? Generally, it is because of the two "thou shalt not" rules: thou shalt not divide by zero, and thou shalt not take the square root of a negative number. So, consider the following three statements.

1. You can't take the square root of a negative number.
2. The domain of the function y= $\sqrt{x}$ is x≥0.
3. The graph of y= $\sqrt{x}$ starts at the y-axis, and goes to the right; it doesn't go to the left. (Draw it.)

Remind them of the “rule of consistency” that we discussed earlier: a function can never take one input and generate two different outputs . Ask them to discuss in pairs, for one minute, how this rule manifests on a graph. Then have class discussion until you have reached the vertical line test.

Come back to the question we started with: why do we graph things? As we demonstrated earlier, graphs enable us to see things visually that are very hard to see in numbers. Draw several different jaggy, shaky graphs, and suggest that they represent the price of gas—ask for verbal descriptions of what each one tells us. Talk again about domain, range, positive, negative.

Throw something straight up into the air and catch it. Tell them there is a function $h\left(t\right)$ that represents the height of that object, as a function of time. (Make sure they get this.) Give them one minute to sketch the graph of that function. Then show them that it is an upside-down parabola (you don’t need to use that word). Emphasize that this does not mean the object traveled in an arc shape: it traveled straight up and down. The horizontal axis is time and the vertical axis is height.

If you have a bit of extra time, explain how to generate graphs (and set the window) on the calculator.

Homework: